共通テスト 数学II・数学B 2024年度追試 第2問 解説

【必答問題】

問題編

問題

　$f(x)=x^3-3x^2+6$ とする。

(1) $f'(x)=\myBox{ア}x^2-\myBox{イ}x$ であるから、 $f(x)$ は $x=\myBox{ウ}$ で極大値 $\myBox{エ}$ をとり、 $x=\myBox{オ}$ で極小値 $\myBox{カ}$ をとる。

　$3\leqq x\leqq 5$ の範囲において、 $f(x)$ は $x=\myBox{キ}$ で最大値をとり、 $x=\myBox{ク}$ で最小値をとる。また、 $1\leqq x\leqq 3$ の範囲において、 $f(x)$ は $x=\myBox{ケ}$ で最大値をとり、 $x=\myBox{コ}$ で最小値をとる。

(2) $t$ を実数とし、 $t\leqq x\leqq t+1$ の範囲における $f(x)$ の最大値を $M(t)$、最小値を $m(t)$ とおく。

　$M(t)=f(t+1)$ かつ $m(t)=f(t)$ となるような $t$ の値の範囲は\[ t\leqq \myBox{サシ},\ \myBox{ス}\leqq t \]である。また、 $M(t)=f(t)$ かつ $m(t)=f(t+1)$ となるような $t$ の値の範囲は\[ \myBox{セ}\leqq t\leqq \myBox{ソ} \]であり。このとき $M(t)-m(t)=f(t)-f(t+1)$ となることに注意すると、 $\mybox{セ}\leqq t\leqq \mybox{ソ}$ の範囲において $M(t)-m(t)$ は $t=\dfrac{\myBox{タ}}{\myBox{チ}}$ で最大値をとることがわかる。

(3) $0\leqq t\leqq 1$ とし、座標平面において2点 $(t,f(t))$, $(t,0)$ を結んでできる線分を $\ell_1$ とおく。 $t$ が $0\leqq t\leqq 1$ の範囲を動くとき、 $\ell_1$ が通過する部分を図示すると図1の灰色部分となる。ただし、境界（境界線）を含む。なお、図1においては関数 $y=f(x)$ のグラフの $0\leqq x\leqq 1$ の部分を実線で表している。

　このとき、図1の灰色の部分の面積は $\dfrac{\myBox{ツテ}}{\myBox{ト}}$ である。

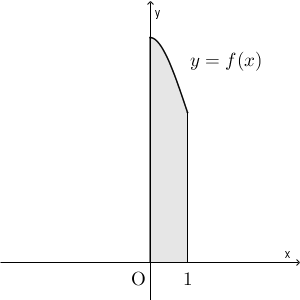
(4) $g(x)=x^3-6x^2+6x+2$ とし、座標平面において2点 $(t,f(t))$, $(t,g(t))$ を結んでできる線分を $\ell_2$ とおく。また、 $r$ を実数とし、実数 $t$ が $r\leqq t\leqq r+1$ の範囲を動くとき、 $\ell_2$ が通過する部分の面積を $S$ とする。

(i) $f(x)-g(x)$ の値は、 $\dBox{ナ}$ 。したがって、すべての実数 $r$ に対して、 $S=\dBox{ニ}$ が成り立つ。

　$\dbox{ナ}$ の解答群

　0: つねに正である
　1: つねに負である
　2: 正になることも、負になることも、 $0$ になることもある

　$\dbox{ニ}$ の解答群

　0: $\int_r^{r+1} f(x) dx$

　1: $\int_r^{r+1} g(x) dx$

　2: $\int_r^{r+1} \{-f(x)\} dx$

　3: $\int_r^{r+1} \{-g(x)\} dx$

　4: $\int_r^{r+1} \{f(x)-g(x)\} dx$

　5: $\int_r^{r+1} \{f(x)+g(x)\} dx$

　6: $\int_r^{r+1} \{g(x)-f(x)\} dx$

　7: $\int_r^{r+1} \{-f(x)-g(x)\} dx$

(ii) $S$ を計算すると\[ S=f(r+1)-f(r)+4 \]となることがわかるので、 $r$ の値が $r=\mybox{セ}$ から $r=\mybox{ソ}$ まで増加するとき、 $S$ の値は $\dBox{ヌ}$ ことがわかる。

　$\dbox{ヌ}$ の解答群

　0: 増加する
　1: 増加してから減少する
　2: 減少する
　3: 減少してから増加する
　4: 一定である

考え方

「線分が通過する領域の面積」という少し変わった聞かれ方をしていますが、図があるのでどういう部分の面積を考えればいいかはすぐにわかるでしょう。

(4)(ii)も重大なヒントが書いてくれていますし、誘導が親切です。だいぶ前に計算した結果をうまく使いながら、省エネで解いていきましょう。

---

【必答問題】

解答編

問題

　$f(x)=x^3-3x^2+6$ とする。

(1) $f'(x)=\myBox{ア}x^2-\myBox{イ}x$ であるから、 $f(x)$ は $x=\myBox{ウ}$ で極大値 $\myBox{エ}$ をとり、 $x=\myBox{オ}$ で極小値 $\myBox{カ}$ をとる。

　$3\leqq x\leqq 5$ の範囲において、 $f(x)$ は $x=\myBox{キ}$ で最大値をとり、 $x=\myBox{ク}$ で最小値をとる。また、 $1\leqq x\leqq 3$ の範囲において、 $f(x)$ は $x=\myBox{ケ}$ で最大値をとり、 $x=\myBox{コ}$ で最小値をとる。

解説

(1)
$f(x)=x^3-3x^2+6$ なので、 $f'(x)=3x^2-6x=3x(x-2)$ となるので、増減表は次のようになります。

\begin{array}{c|ccccc} x & \cdots & 0 & \cdots & 2 & \cdots \\ \hline f'(x) & + & 0 & - & 0 & + \\ \hline f(x) & \nearrow & & \searrow & & \nearrow & \end{array}

これより、 $x=0$ で極大値 $6$ をとり、 $x=2$ で極小値 $2$ をとることがわかります。

$3\leqq x\leqq 5$ の範囲では単調増加なので、 $x=5$ のときに最大値をとり、 $x=3$ のときに最小値をとることがわかります。

$1\leqq x\leqq 3$ の範囲では、最大値をとる候補は両端の $x=1,3$ です。それぞれの値を計算すると $f(1)=1-3+6=4$ と $f(3)=6$ なので、 $x=3$ のときに最大値をとることがわかります。また、 $x=2$ で最小値を取ります。

ちなみに、解答欄を見れば、キとクに入るのは $3,4,5$ のどれかだし、ケとコに入るのは $1,2,3$ のどれかなので、ここの答えだけを出すだけなら、全部代入して確かめる、という方法もあります。

解答

アイ：36 (2点)
ウエ：06 (2点)
オカ：22 (2点)
キク：53 (2点)
ケコ：32 (2点)

解答編　つづき

問題

(2) $t$ を実数とし、 $t\leqq x\leqq t+1$ の範囲における $f(x)$ の最大値を $M(t)$、最小値を $m(t)$ とおく。

　$M(t)=f(t+1)$ かつ $m(t)=f(t)$ となるような $t$ の値の範囲は\[ t\leqq \myBox{サシ},\ \myBox{ス}\leqq t \]である。また、 $M(t)=f(t)$ かつ $m(t)=f(t+1)$ となるような $t$ の値の範囲は\[ \myBox{セ}\leqq t\leqq \myBox{ソ} \]であり。このとき $M(t)-m(t)=f(t)-f(t+1)$ となることに注意すると、 $\mybox{セ}\leqq t\leqq \mybox{ソ}$ の範囲において $M(t)-m(t)$ は $t=\dfrac{\myBox{タ}}{\myBox{チ}}$ で最大値をとることがわかる。

解説

(2)
$M(t)=f(t+1)$ かつ $m(t)=f(t)$ になるとは、 $t\leqq x\leqq t+1$ の区間で単調増加になっているということです。増減表は先ほど求めた通り次のようになります。

\begin{array}{c|ccccc} x & \cdots & 0 & \cdots & 2 & \cdots \\ \hline f'(x) & + & 0 & - & 0 & + \\ \hline f(x) & \nearrow & & \searrow & & \nearrow & \end{array}

これを見ると、 $t\leqq x\leqq t+1$ の区間で単調増加となるような範囲は、 $t+1$ が $0$ 以下の部分、つまり、 $t\leqq -1$ の範囲と、 $t$ が $2$ 以上の部分です。つまり、 $t\leqq -1$ または $2\leqq t$ となります。

$M(t)=f(t)$ かつ $m(t)=f(t+1)$ になるとは、 $t\leqq x\leqq t+1$ の区間で単調減少になっているということです。先ほどの増減表から、 $t\geqq 0$ かつ $t+1\leqq 2$ の場合です。つまり、 $0\leqq t\leqq 1$ のときだとわかります。

このとき、
\begin{eqnarray} & & M(t)-m(t) \\[5pt] &=& f(t)-f(t+1) \\[5pt] &=& (t^3-3t^2+6)-\{(t+1)^3-3(t+1)^2+6\} \\[5pt] &=& (t^3-3t^2+6)-(t^3+3t^2+3t+1-3t^2-6t-3+6) \\[5pt] &=& (t^3-3t^2+6)-(t^3-3t+4) \\[5pt] &=& -3t^2+3t+2 \\[5pt] &=& -3\left(t-\frac{1}{2}\right)^2+\frac{3}{4}+2 \\[5pt] \end{eqnarray}なので、 $0\leqq t\leqq 1$ の範囲では $M(t)-m(t)$ は $t=\dfrac{1}{2}$ のときに最大値をとることがわかります。

解答

サシス：-12 (2点)
セソ：01 (2点)
タチ：12 (2点)

解答編　つづき

問題

(3) $0\leqq t\leqq 1$ とし、座標平面において2点 $(t,f(t))$, $(t,0)$ を結んでできる線分を $\ell_1$ とおく。 $t$ が $0\leqq t\leqq 1$ の範囲を動くとき、 $\ell_1$ が通過する部分を図示すると図1の灰色部分となる。ただし、境界（境界線）を含む。なお、図1においては関数 $y=f(x)$ のグラフの $0\leqq x\leqq 1$ の部分を実線で表している。

　このとき、図1の灰色の部分の面積は $\dfrac{\myBox{ツテ}}{\myBox{ト}}$ である。

解説

(3)
求めるものは、 $y=f(x)$ の $0\leqq x\leqq 1$ の部分、 $x$ 軸、 $y$ 軸、 $x=1$ で囲まれた部分の面積なので
\begin{eqnarray} & & \int_0^1 f(x) dx \\[5pt] &=& \int_0^1 (x^3-3x^2+6) dx \\[5pt] &=& \left[\frac{x^4}{4}-x^3+6x\right]_0^1 \\[5pt] &=& \frac{1}{4}-1+6=\frac{21}{4} \end{eqnarray}となります。

解答

ツテト：214 (4点)

解答編　つづき

問題

(4) $g(x)=x^3-6x^2+6x+2$ とし、座標平面において2点 $(t,f(t))$, $(t,g(t))$ を結んでできる線分を $\ell_2$ とおく。また、 $r$ を実数とし、実数 $t$ が $r\leqq t\leqq r+1$ の範囲で動くとき、 $\ell_2$ が通過する部分の面積を $S$ とする。

(i) $f(x)-g(x)$ の値は、 $\dBox{ナ}$ 。したがって、すべての実数 $r$ に対して、 $S=\dBox{ニ}$ が成り立つ。

　$\dBox{ナ}$ の解答群

　0: つねに正である
　1: つねに負である
　2: 正になることも、負になることも、 $0$ になることもある

　$\dBox{ニ}$ の解答群

　0: $\int_r^{r+1} f(x) dx$

　1: $\int_r^{r+1} g(x) dx$

　2: $\int_r^{r+1} \{-f(x)\} dx$

　3: $\int_r^{r+1} \{-g(x)\} dx$

　4: $\int_r^{r+1} \{f(x)-g(x)\} dx$

　5: $\int_r^{r+1} \{f(x)+g(x)\} dx$

　6: $\int_r^{r+1} \{g(x)-f(x)\} dx$

　7: $\int_r^{r+1} \{-f(x)-g(x)\} dx$

解説

(4)
(i)
\begin{eqnarray} & & f(x)-g(x) \\[5pt] &=& (x^3-3x^2+6)-(x^3-6x^2+6x+2) \\[5pt] &=& 3x^2-6x+4 \\[5pt] &=& 3(x-1)^2+1 \\[5pt] \end{eqnarray}なので、 $f(x)-g(x)$ はつねに正であることがわかります。

これより、面積 $S$ は\[ S=\int_r^{r+1} \{f(x)-g(x)\}dx \]となります。

$f(x)-g(x)$ が正か負かを調べるということは、グラフでいうと、どちらが上かを考えていることになります。これによって面積を出すときに、 $f(x)-g(x)$ を積分するのか、 $g(x)-f(x)$ を積分するのかが変わってきます。

解答

ナ：0 (3点)
ニ：4 (3点)

解答編　つづき

問題

(ii) $S$ を計算すると\[ S=f(r+1)-f(r)+4 \]となることがわかるので、 $r$ の値が $r=\mybox{セ}$ から $r=\mybox{ソ}$ まで増加するとき、 $S$ の値は $\dBox{ヌ}$ ことがわかる。

　$\dbox{ヌ}$ の解答群

　0: 増加する
　1: 増加してから減少する
　2: 減少する
　3: 減少してから増加する
　4: 一定である

解説

(ii)
まず、問題文に書いていることを確認します。

(4)(i)で計算したように、 $f(x)-g(x)=3x^2-6x+4$ です。(1)で計算したように、 $f'(x)=3x^2-6x$ なので、 $f(x)-g(x)=f'(x)+4$ が成り立ちます。これより、 $S$ を計算すると
\begin{eqnarray} S &=& \int_r^{r+1} \{f(x)-g(x)\}dx \\[5pt] &=& \int_r^{r+1} \{f'(x)+4\}dx \\[5pt] &=& [f(x)+4x]_r^{r+1} \\[5pt] &=& f(r+1)-f(r)+4(r+1)-4r \\[5pt] &=& f(r+1)-f(r)+4 \\[5pt] \end{eqnarray}となり、問題文に書いてあることが確認できました。

(2)で、 $f(t)-f(t+1)=-3t^2+3t+2$ と計算していたので、
\begin{eqnarray} & & f(r+1)-f(r)+4 \\[5pt] &=& (3r^2-3r-2)+4 \\[5pt] &=& 3\left(r-\frac{1}{2}\right)^2-\frac{3}{4}+2 \\[5pt] \end{eqnarray}となるので、 $r=0$ から $r=1$ まで増加するとき、 $S$ の値は減少してから増加することがわかります。

解答

ヌ：3 (4点)