共通テスト 数学I・数学A 2024年度追試 第5問 解説
【第3問~第5問から2問選択】
問題編
問題
三角形の各頂点から向かい合う辺またはその延長に下ろした三つの垂線は1点で交わることが知られている。この点を三角形の垂心という。
$\triangle\mathrm{ABC}$ の外心を $\mathrm{O}$、垂心を $\mathrm{H}$、内心を $\mathrm{I}$ とする。点 $\mathrm{O}$ に関して、点 $\mathrm{A,B,C}$ と対称な点を、それぞれ $\mathrm{P,Q,R}$ とする。直線 $\mathrm{AH}$ と直線 $\mathrm{BC}$ との交点を $\mathrm{D}$、直線 $\mathrm{BH}$ と直線 $\mathrm{AC}$ との交点を $\mathrm{E}$ とする。
(1) $\triangle\mathrm{ABC}$ を三つの辺の長さがすべて異なる鋭角三角形とする。
(i) 直線 $\mathrm{AC}$ は、三つの直線 $\mathrm{AR,CP}, \dBox{ア}$ のそれぞれと垂直である。また、直線 $\mathrm{BC}$ は、三つの直線 $\mathrm{AH,BR},\dBox{イ}$ のそれぞれと垂直である。
$\dbox{ア},\dbox{イ}$ の解答群(同じものを繰り返し選んでもよい。)
0: $\mathrm{AO}$
1: $\mathrm{AQ}$
2: $\mathrm{BH}$
3: $\mathrm{BO}$
4: $\mathrm{CH}$
5: $\mathrm{CO}$
6: $\mathrm{CQ}$
7: $\mathrm{HO}$
参考図 (ii) $\mathrm{BD:DC}=4:1$ および $\mathrm{AE:EC}=2:3$ であるとする。 $\triangle \mathrm{ADC}$ と直線 $\mathrm{BE}$ に着目すると\[ \frac{\mathrm{AH}}{\mathrm{HD}}=\frac{\myBox{ウ}}{\myBox{エ}} \]である。よって、このことと(i)から、 $\triangle\mathrm{ARB}$ の面積は $\triangle \mathrm{ABC}$ の面積の $\dfrac{\myBox{オ}}{\myBox{カキ}}$ 倍であることがわかる。
(2) $\triangle \mathrm{ABC}$ を三つの辺の長さがすべて異なる鋭角三角形とする。このとき、 $\triangle \mathrm{ABP}$ と $\dBox{ク}$ は相似である。なぜならば、 $\triangle \mathrm{ABP}$ と $\dbox{ク}$ はいずれも直角三角形であり、また、 $\angle \mathrm{APB}=\dBox{ケ}$ が成り立つからである。
このことから、外心 $\mathrm{O}$、垂心 $\mathrm{H}$、内心 $\mathrm{I}$ について次の命題(a), (b)の真偽の組合せとして正しいものは $\dBox{コ}$ であることがわかる。
(a) 直線 $\mathrm{AO}$ と直線 $\mathrm{AH}$ は直線 $\mathrm{AI}$ に関して対称である。
(b) 外心 $\mathrm{O}$ と垂心 $\mathrm{H}$ は直線 $\mathrm{AI}$ に関して対称である。$\dbox{ク}$ の解答群
0: $\triangle\mathrm{ACP}$
1: $\triangle\mathrm{ADC}$
2: $\triangle\mathrm{BPC}$
3: $\triangle\mathrm{PHC}$$\dbox{ケ}$ の解答群
0: $\angle \mathrm{ACD}$
1: $\angle \mathrm{BHC}$
2: $\angle \mathrm{CAP}$
3: $\angle \mathrm{CBP}$$\dbox{コ}$ の解答群
0: (a)真 (b)真
1: (a)真 (b)偽
2: (a)偽 (b)真
3: (a)偽 (b)偽(3) $\triangle\mathrm{ABC}$ を三つの辺の長さがすべて異なる鈍角三角形で、 $\angle \mathrm{BAC}$ が鈍角であるものとする。このとき\[ \angle\mathrm{BAP}=\dBox{サ} \]および\[ \angle\mathrm{OAI}+\dBox{シ}=180^{\circ} \]がつねに成り立つ。なお、角の大きさはすべて $0^{\circ}$ より大きく $180^{\circ}$ 以下で考えるものとする。
$\dbox{サ}$ の解答群
0: $\angle\mathrm{ACH}$
1: $\angle\mathrm{ADC}$
2: $\angle\mathrm{CAD}$
3: $\angle\mathrm{CAI}$$\dbox{シ}$ の解答群
0: $\angle\mathrm{HAB}$
1: $\angle\mathrm{HAC}$
2: $\angle\mathrm{HAI}$
3: $\angle\mathrm{HAO}$
考え方
(1)(ii)は、(i)を使うと書いていますが、どう使うかは少し難しいかもしれません。三角形 $\mathrm{ARB}$ の面積を直接求めるのは難しいので、これと同じ面積の三角形がないか、考えてみましょう。
(2)も、後半では前半を使いますが、どう使うかはわかりにくいかもしれません。内心の性質を思い出しましょう。
(3)は、鈍角の場合の図を正確にかくのが難しいため、なかなか大変だと思います。特に、垂心の位置がどうなるかはよく考えましょう。
【第3問~第5問から2問選択】
解答編
問題
三角形の各頂点から向かい合う辺またはその延長に下ろした三つの垂線は1点で交わることが知られている。この点を三角形の垂心という。
$\triangle\mathrm{ABC}$ の外心を $\mathrm{O}$、垂心を $\mathrm{H}$、内心を $\mathrm{I}$ とする。点 $\mathrm{O}$ に関して、点 $\mathrm{A,B,C}$ と対称な点を、それぞれ $\mathrm{P,Q,R}$ とする。直線 $\mathrm{AH}$ と直線 $\mathrm{BC}$ との交点を $\mathrm{D}$、直線 $\mathrm{BH}$ と直線 $\mathrm{AC}$ との交点を $\mathrm{E}$ とする。
(1) $\triangle\mathrm{ABC}$ を三つの辺の長さがすべて異なる鋭角三角形とする。
(i) 直線 $\mathrm{AC}$ は、三つの直線 $\mathrm{AR,CP}, \dBox{ア}$ のそれぞれと垂直である。また、直線 $\mathrm{BC}$ は、三つの直線 $\mathrm{AH,BR},\dBox{イ}$ のそれぞれと垂直である。
$\dbox{ア},\dbox{イ}$ の解答群(同じものを繰り返し選んでもよい。)
0: $\mathrm{AO}$
1: $\mathrm{AQ}$
2: $\mathrm{BH}$
3: $\mathrm{BO}$
4: $\mathrm{CH}$
5: $\mathrm{CO}$
6: $\mathrm{CQ}$
7: $\mathrm{HO}$
参考図
解説
(1)
(i)
点 $\mathrm{O}$ は $\triangle\mathrm{ABC}$ の外心なので、線分 $\mathrm{AP,BQ,CR}$ は外接円の直径です。
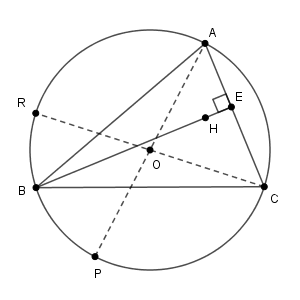
なので、 $\mathrm{AC}\perp\mathrm{AR}$, $\mathrm{AC}\perp\mathrm{CP}$ がわかります。また、 $\mathrm{H}$ は垂心なので、 $\mathrm{AC}\perp\mathrm{BH}$ となります。
もう一度、直径に着目すると、 $\mathrm{BC}\perp\mathrm{BR}$, $\mathrm{BC}\perp\mathrm{CQ}$ がわかります。
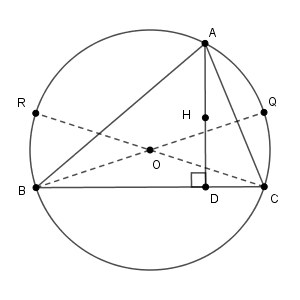
また、 $\mathrm{H}$ は垂心なので、 $\mathrm{BC}\perp\mathrm{AH}$ となります。
解答
ア:2 (2点)
イ:6 (2点)
解答編 つづき
問題
(ii) $\mathrm{BD:DC}=4:1$ および $\mathrm{AE:EC}=2:3$ であるとする。 $\triangle \mathrm{ADC}$ と直線 $\mathrm{BE}$ に着目すると\[ \frac{\mathrm{AH}}{\mathrm{HD}}=\frac{\myBox{ウ}}{\myBox{エ}} \]である。よって、このことと(i)から、 $\triangle\mathrm{ARB}$ の面積は $\triangle \mathrm{ABC}$ の面積の $\dfrac{\myBox{オ}}{\myBox{カキ}}$ 倍であることがわかる。
解説
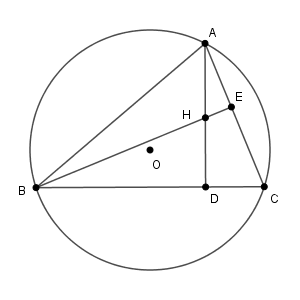
$\triangle \mathrm{ADC}$ と直線 $\mathrm{BE}$ に着目して、メネラウスの定理から
\begin{eqnarray}
\frac{\mathrm{AH}}{\mathrm{HD}} \cdot \frac{\mathrm{DB}}{\mathrm{BC}} \cdot \frac{\mathrm{CE}}{\mathrm{EA}} &=& 1 \\[5pt]
\frac{\mathrm{AH}}{\mathrm{HD}} \cdot \frac{4}{5} \cdot \frac{3}{2} &=& 1 \\[5pt]
\frac{\mathrm{AH}}{\mathrm{HD}} &=& \frac{5}{6} \\[5pt]
\end{eqnarray}となります。
次に、 $\triangle\mathrm{ARB}$ の面積と $\triangle \mathrm{ABC}$ の面積について考えます。
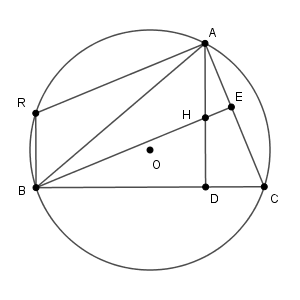
(i)で見たように、直線 $\mathrm{AR,BH}$ は直線 $\mathrm{AC}$ に垂直なので、この2直線は平行です。また、直線 $\mathrm{AH,BR}$ は直線 $\mathrm{BC}$ に垂直なので、この2直線も平行です。なので、四角形 $\mathrm{ARBH}$ は平行四辺形だから、 $\triangle\mathrm{ARB}$ の面積は $\triangle\mathrm{AHB}$ の面積と等しくなります。
$\triangle\mathrm{AHB}$ の面積は $\triangle\mathrm{ADB}$ の面積の $\dfrac{\mathrm{AH}}{\mathrm{AD}}$ 倍であり、 $\triangle\mathrm{ADB}$ の面積は $\triangle\mathrm{ABC}$ の面積の $\dfrac{\mathrm{BD}}{\mathrm{BC}}$ 倍なので、$\triangle\mathrm{ARB}$ の面積は $\triangle\mathrm{ABC}$ の面積の
\begin{eqnarray}
\dfrac{\mathrm{AH}}{\mathrm{AD}} \cdot \dfrac{\mathrm{BD}}{\mathrm{BC}} &=& \frac{5}{5+6}\cdot\frac{4}{5}=\frac{4}{11}
\end{eqnarray}倍だとわかります。
解答
ウエ:56 (3点)
オカキ:411 (3点)
解答編 つづき
問題
(2) $\triangle \mathrm{ABC}$ を三つの辺の長さがすべて異なる鋭角三角形とする。このとき、 $\triangle \mathrm{ABP}$ と $\dBox{ク}$ は相似である。なぜならば、 $\triangle \mathrm{ABP}$ と $\dbox{ク}$ はいずれも直角三角形であり、また、 $\angle \mathrm{APB}=\dBox{ケ}$ が成り立つからである。
このことから、外心 $\mathrm{O}$、垂心 $\mathrm{H}$、内心 $\mathrm{I}$ について次の命題(a), (b)の真偽の組合せとして正しいものは $\dBox{コ}$ であることがわかる。
(a) 直線 $\mathrm{AO}$ と直線 $\mathrm{AH}$ は直線 $\mathrm{AI}$ に関して対称である。
(b) 外心 $\mathrm{O}$ と垂心 $\mathrm{H}$ は直線 $\mathrm{AI}$ に関して対称である。$\dbox{ク}$ の解答群
0: $\triangle\mathrm{ACP}$
1: $\triangle\mathrm{ADC}$
2: $\triangle\mathrm{BPC}$
3: $\triangle\mathrm{PHC}$$\dbox{ケ}$ の解答群
0: $\angle \mathrm{ACD}$
1: $\angle \mathrm{BHC}$
2: $\angle \mathrm{CAP}$
3: $\angle \mathrm{CBP}$$\dbox{コ}$ の解答群
0: (a)真 (b)真
1: (a)真 (b)偽
2: (a)偽 (b)真
3: (a)偽 (b)偽
解説
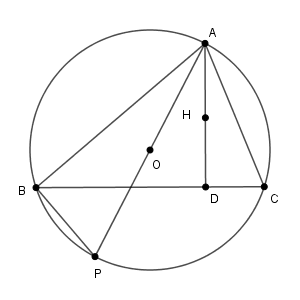
$\triangle \mathrm{ABP}$ と $\triangle \mathrm{ADC}$ について、 $\angle\mathrm{ABP}$ は直角で(線分 $\mathrm{AP}$ は直径なので)、 $\angle \mathrm{ADC}$ も直角です。また、弧 $\mathrm{AB}$ に対する円周角だから、 $\angle\mathrm{APB}=\angle\mathrm{ACD}$ も成り立つので、$\triangle \mathrm{ABP}$ と $\triangle \mathrm{ADC}$ は相似だとわかります。
内心 $\mathrm{I}$ は、 $\angle\mathrm{BAC}$ の二等分線上にあります。また、先ほど相似と示したことから、 $\angle\mathrm{BAP}=\angle\mathrm{DAC}$ が成り立つので、 $\mathrm{I}$ は $\angle\mathrm{OAH}$ の二等分線上にあります。つまり、直線 $\mathrm{AO}$ と直線 $\mathrm{AH}$ が直線 $\mathrm{AI}$ に関して対称である、ということです。
$\mathrm{O,H}$ が直線 $\mathrm{AI}$ に関して対称なら、 $\mathrm{AO=AH}$ となりますが、図からそうはならないので、これは偽です。 $\mathrm{A}$ を円周上を動かしたときに、 $\mathrm{AH}$ の長さは変わるのに $\mathrm{AO}$ の長さは変わらない、と考えてもいいです。
解答
クケ:10 (3点)
コ:1 (3点)
解答編 つづき
問題
(3) $\triangle\mathrm{ABC}$ を三つの辺の長さがすべて異なる鈍角三角形で、 $\angle \mathrm{BAC}$ が鈍角であるものとする。このとき\[ \angle\mathrm{BAP}=\dBox{サ} \]および\[ \angle\mathrm{OAI}+\dBox{シ}=180^{\circ} \]がつねに成り立つ。なお、角の大きさはすべて $0^{\circ}$ より大きく $180^{\circ}$ 以下で考えるものとする。
$\dbox{サ}$ の解答群
0: $\angle\mathrm{ACH}$
1: $\angle\mathrm{ADC}$
2: $\angle\mathrm{CAD}$
3: $\angle\mathrm{CAI}$$\dbox{シ}$ の解答群
0: $\angle\mathrm{HAB}$
1: $\angle\mathrm{HAC}$
2: $\angle\mathrm{HAI}$
3: $\angle\mathrm{HAO}$
解説
図は次のようになります。垂心 $\mathrm{H}$ は三角形の外にあります。
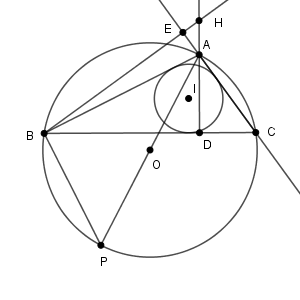
この場合でも、$\angle\mathrm{ABP}$ と $\angle\mathrm{ADC}$ は直角です。また、 $\angle\mathrm{BPA}$ と $\angle\mathrm{DCA}$ は弧 $\mathrm{AB}$ に対する円周角です。なので、 $\angle\mathrm{BAP}=\angle\mathrm{CAD}$ がつねに成り立ちます。
また、このことと、 $\angle\mathrm{BAI}=\angle\mathrm{CAI}$ から、 $\angle\mathrm{OAI}=\angle\mathrm{DAI}$ がいえます。 $\angle\mathrm{DAI}+\angle\mathrm{HAI}=180^{\circ}$ より、\[ \angle\mathrm{OAI}+\angle\mathrm{HAI}=180^{\circ} \]が成り立ちます。
解答
サ:2 (2点)
シ:2 (2点)





