共通テスト 数学I・数学A 2024年度追試 第3問 解説
【第3問~第5問から2問選択】
問題編
問題
1辺の長さが $1$ である正方形のタイルが6枚ある。これらのタイルを1枚ずつ互いに重ならないように、1辺の長さが $4$ である正方形の壁に貼っていくことを考える。ただし、新しく貼るタイルは、その左側と下側が壁の縁やすでに貼られているタイルとの間に隙間ができないように、詰めて貼られるものとする。また、新しく貼るタイルの位置の候補が全部で $n$ 箇所あるとき、そのうちのどの位置についてもタイルを貼る確率は $\dfrac{1}{n}$ であるものとする。
このとき、1枚目のタイルは壁の左下の隅に貼られることになる。また、2枚目のタイルの貼る位置の候補は、1枚目のタイルのすぐ右かすぐ上の2箇所となる。
同様に考えると、4枚目のタイルを貼るまでのタイルの配置は、図1のようになる。ただし、図1における矢印はタイル配置の推移を表している。なお、3枚目から4枚目の間の矢印は省略している。
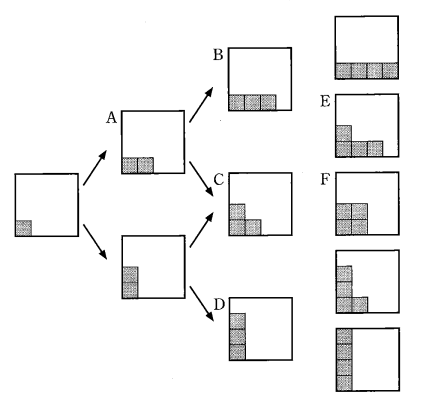
図1 以下、タイルの配置を、単に配置という。
(1) 2枚目のタイルを貼った時点での配置を考える。
2枚目のタイルを貼った時点で配置が図1のAになる確率は $\dfrac{\myBox{ア}}{\myBox{イ}}$ である。
(2) 3枚目のタイルを貼った時点での配置を考える。
3枚目のタイルを貼った時点での配置が図1のBになる確率は $\dfrac{\mybox{ア}}{\mybox{イ}} \times \dfrac{\myBox{ウ}}{\myBox{エ}}=\dfrac{\myBox{オ}}{\myBox{カ}}$ である。
また、3枚目のタイルを貼った時点での配置が図1のCになる確率は $\dfrac{\myBox{キ}}{\myBox{ク}}$ である。
(3) 4枚目のタイルを貼った時点での配置を考える。ここで、図1を再掲しておく。

図1(再掲) (i) 4枚目のタイルを貼った時点での配置が図1のEとなるとき、3枚目のタイルを貼った時点でのあり得る配置は、図1のB, C, Dのうち $\dBox{ケ}$ である。したがって、4枚目のタイルを貼った時点での配置が図1のEとなる確率は $\dfrac{\myBox{コ}}{\myBox{サシ}}$ である。
4枚目のタイルを貼った時点での配置が図1のFとなるとき、3枚目のタイルを貼った時点でのあり得る配置は、図1のB, C, Dのうち $\dBox{ス}$ である。したがって、4枚目のタイルを貼った時点での配置が図1のFとなる確率は $\dfrac{\myBox{セ}}{\myBox{ソ}}$ である。
$\dbox{ケ}$, $\dbox{ス}$ の解答群(同じものを繰り返し選んでもよい。)
0: Bだけ
1: Cだけ
2: Dだけ
3: BとCだけ
4: BとDだけ
5: CとDだけ
6: BとCとDのすべて(ii) 4枚目のタイルを貼った時点での配置が図1のEであったとき、2枚目のタイルを貼った時点での配置が図1のAである条件付き確率は $\dfrac{\myBox{タ}}{\myBox{チ}}$ である。
(4) 6枚目のタイルを貼った時点での配置を考える。
6枚目のタイルを貼った時点での配置が図2となる確率は $\dfrac{\myBox{ツ}}{\myBox{テト}}$ である。

図2
考え方
確率の問題としては難しくないのですが、どこに配置できるかを正しく把握すのは少し難しいです。隙間があってはいけないことに注意しましょう。
【第3問~第5問から2問選択】
解答編
問題
1辺の長さが $1$ である正方形のタイルが6枚ある。これらのタイルを1枚ずつ互いに重ならないように、1辺の長さが $4$ である正方形の壁に貼っていくことを考える。ただし、新しく貼るタイルは、その左側と下側が壁の縁やすでに貼られているタイルとの間に隙間ができないように、詰めて貼られるものとする。また、新しく貼るタイルの位置の候補が全部で $n$ 箇所あるとき、そのうちのどの位置についてもタイルを貼る確率は $\dfrac{1}{n}$ であるものとする。
このとき、1枚目のタイルは壁の左下の隅に貼られることになる。また、2枚目のタイルの貼る位置の候補は、1枚目のタイルのすぐ右かすぐ上の2箇所となる。
同様に考えると、4枚目のタイルを貼るまでのタイルの配置は、図1のようになる。ただし、図1における矢印はタイル配置の推移を表している。なお、3枚目から4枚目の間の矢印は省略している。

図1 以下、タイルの配置を、単に配置という。
(1) 2枚目のタイルを貼った時点での配置を考える。
2枚目のタイルを貼った時点で配置が図1のAになる確率は $\dfrac{\myBox{ア}}{\myBox{イ}}$ である。
解説
(1)
1枚目を貼る場所は壁の左下で、2枚目はそのすぐ右か上の2通りです。Aになるのはすぐ右を選んだときなので、こうなる確率は $\dfrac{1}{2}$ となります。
解答
アイ:12 (2点)
解答編 つづき
問題
(2) 3枚目のタイルを貼った時点での配置を考える。
3枚目のタイルを貼った時点での配置が図1のBになる確率は $\dfrac{\mybox{ア}}{\mybox{イ}} \times \dfrac{\myBox{ウ}}{\myBox{エ}}=\dfrac{\myBox{オ}}{\myBox{カ}}$ である。
また、3枚目のタイルを貼った時点での配置が図1のCになる確率は $\dfrac{\myBox{キ}}{\myBox{ク}}$ である。
解説
(2)
2枚目を1枚目のすぐ右に貼った場合、3枚目は「1枚目の上」「2枚目の右」の2通りの置き方があります(「2枚目の上」は左側に壁との隙間ができるのでダメです)。2枚目を1枚目のすぐ上に貼った場合、3枚目は「1枚目の右」「2枚目の上」の2通りの置き方があります。
このうち、Bの配置になるには、「2枚目は1枚目の右」「3枚目は2枚目の右」の場合だけなので、こうなる確率は\[ \frac{1}{2}\times\frac{1}{2}=\frac{1}{4} \]となります。
Cの配置になるには、
・「2枚目は1枚目の右」「3枚目は1枚目の上」
・「2枚目は1枚目の上」「3枚目は1枚目の右」
の2通りがあります。なので、こうなる確率は\[ \frac{1}{2}\times\frac{1}{2}+\frac{1}{2}\times\frac{1}{2}=\frac{1}{2} \]となります。
なお、対称性からDの配置になる確率はBの配置になる確率と同じ $\dfrac{1}{4}$ なので、Cの配置になる確率を\[ 1-\frac{1}{4}-\frac{1}{4}=\frac{1}{2} \]と求めることもできます。
解答
ウエオカ:1214 (2点)
キク:12 (2点)
解答編 つづき
問題
(3) 4枚目のタイルを貼った時点での配置を考える。ここで、図1を再掲しておく。

図1(再掲) (i) 4枚目のタイルを貼った時点での配置が図1のEとなるとき、3枚目のタイルを貼った時点でのあり得る配置は、図1のB, C, Dのうち $\dBox{ケ}$ である。したがって、4枚目のタイルを貼った時点での配置が図1のEとなる確率は $\dfrac{\myBox{コ}}{\myBox{サシ}}$ である。
4枚目のタイルを貼った時点での配置が図1のFとなるとき、3枚目のタイルを貼った時点でのあり得る配置は、図1のB, C, Dのうち $\dBox{ス}$ である。したがって、4枚目のタイルを貼った時点での配置が図1のFとなる確率は $\dfrac{\myBox{セ}}{\myBox{ソ}}$ である。
$\dbox{ケ}$, $\dbox{ス}$ の解答群(同じものを繰り返し選んでもよい。)
0: Bだけ
1: Cだけ
2: Dだけ
3: BとCだけ
4: BとDだけ
5: CとDだけ
6: BとCとDのすべて
解説
(3)
(i)
Eの配置になるには、Bの配置から「4枚目は1枚目の上」となる場合と、Cの配置から「4枚目は1枚目の右の右」となる場合のみです。なので、3枚目としてありえるのは、BとCの配置です。
Bの配置のとき、4枚目の場所の候補は2つです(1枚目の上、3枚目の右)。また、Cの配置のとき、4枚目の候補は3つです(1枚目の上の上、1枚目の右上、1枚目の右の右)。よって、Eの配置になる確率は\[ \frac{1}{4}\cdot\frac{1}{2}+\frac{1}{2}\cdot\frac{1}{3}=\frac{3+4}{24}=\frac{7}{24} \]となります。
Fの配置になるには、Cの配置から「4枚目は1枚目の右上」となる場合のみです。なので、3枚目としてあり得るのは、Cの配置のみです。BもDも、Fからはみ出るタイルがあるのでダメです。
また、Fの配置になる確率は\[ \frac{1}{2}\cdot\frac{1}{3}=\frac{1}{6} \]となります。
解答
ケコサシ:3724 (3点)
スセソ:116 (3点)
解答編 つづき
問題
(ii) 4枚目のタイルを貼った時点での配置が図1のEであったとき、2枚目のタイルを貼った時点での配置が図1のAである条件付き確率は $\dfrac{\myBox{タ}}{\myBox{チ}}$ である。
解説
(ii)
(i)で求めた通り、Eの配置になる確率は $\dfrac{7}{24}$ です。2枚目の時点でAの配置、かつ、4枚目でEの配置になる確率は、3枚目がBかCかで分けて考えると\[ \frac{1}{2}\cdot\frac{1}{2}\cdot\frac{1}{2}+\frac{1}{2}\cdot\frac{1}{2}\cdot\frac{1}{3}=\frac{1}{8}+\frac{1}{12}=\frac{5}{24} \]となります。なので、求める条件付き確率は\[ \frac{5}{24} \div \frac{7}{24}=\frac{5}{7} \]となります。
解答
タチ:57 (4点)
解答編 つづき
問題
(4) 6枚目のタイルを貼った時点での配置を考える。
6枚目のタイルを貼った時点での配置が図2となる確率は $\dfrac{\myBox{ツ}}{\myBox{テト}}$ である。

図2
解説
(4)
図2のようになるには、
4枚目を並べた時点で、EかFかFの下の状態にならないといけません。なお、対称性から、Fの下の状態になる確率は、Eの状態になる確率と等しいことがわかります。
4枚目がEだった場合、「1枚目の上の上」「1枚目の右上」に貼ればよく、どちらを先に貼るかを考えれば、図2のようになる確率は\[ \frac{7}{24}\cdot\left(\frac{1}{3}\cdot\frac{1}{3}+\frac{1}{3}\cdot\frac{1}{3} \right)=\frac{14}{216} \]となります。
4枚目がFだった場合、「1枚目の上の上」「1枚目の右の右」に貼ればよく、どちらを先に貼るかを考えれば、図2のようになる確率は\[ \frac{1}{6}\cdot\left(\frac{1}{2}\cdot\frac{1}{3}+\frac{1}{2}\cdot\frac{1}{3} \right)=\frac{1}{18} \]となります。
よって、図2のようになる確率は\[ 2\cdot\frac{14}{216}+\frac{1}{18}=\frac{14+6}{108}=\frac{5}{27} \]となります。
解答
ツテト:527 (4点)





