共通テスト 数学I・数学A 2024年度追試 第2問 [1] 解説
【必答問題】
問題編
問題
花子さんと太郎さんは、絶対値を含む関数のグラフについて考えている。
(1) 関数\[ y=\frac{1}{8}|x^2+2x-8|+\frac{1}{8}(x^2-6x) \quad \cdots ① \]のグラフを考える。
(i) 2次不等式 $x^2+2x-8\lt 0$ の解は $\myBox{アイ}\lt x\lt\myBox{ウ}$ である。
$\mybox{アイ}\lt x\lt\mybox{ウ}$ のとき、 $x^2+2x-8$ の値は負となるので、①は\[ y=-\frac{1}{8}(x^2+2x-8)+\frac{1}{8}(x^2-6x)=-x+1 \]と変形できる。
$x\leqq \mybox{アイ}$, $\mybox{ウ}\leqq x$ のとき、①は\[ y=\frac{1}{8}(x^2+2x-8)+\frac{1}{8}(x^2-6x)=\frac{1}{4}x^2-\frac{1}{2}x-1 \]と変形できる。
(ii) 2次関数\[ y=\frac{1}{4}x^2-\frac{1}{2}x-1 \]のグラフの頂点の座標は $\left(\myBox{エ},\dfrac{\myBox{オカ}}{\myBox{キ}}\right)$ である。
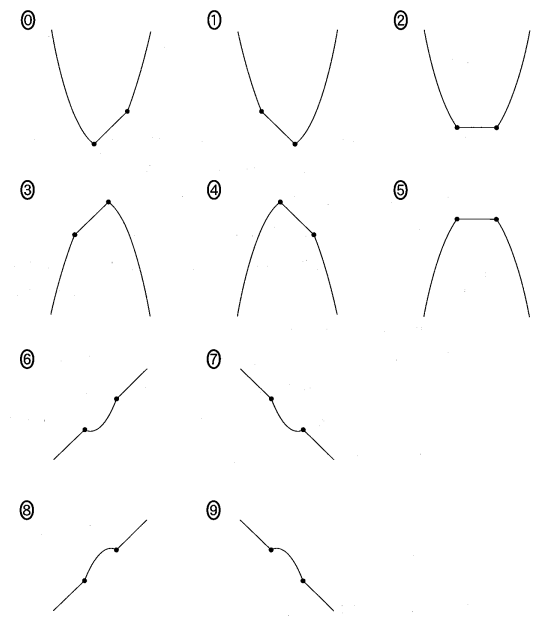
(iii) ①のグラフは $\dBox{ク}$ である。
$\dbox{ク}$ については、最も適当なものを次の 0 ~ 9 のうちから一つ選べ。なお、 $x$ 軸と $y$ 軸は省略してあるが、 $x$ 軸は右方向、 $y$ 軸は上方向がそれぞれ正の方向である。
(2) 花子さんと太郎さんは、(1)を振り返って、グラフのおおよその形をより簡単に知る手順を、関数\[ y=-\frac{1}{8}|x^2-9|-\frac{1}{8}x^2+x \quad \cdots ② \]を例にして考えている。
- ①の関数のグラフを考えるのは大変だったね。おおよその形でよいから、あまり計算せずに簡単に知ることはできないかな。
- ②の関数も①の関数と同じように $x^2$ の項が消えて1次関数となるような $x$ の値の範囲があるね。具体的には、 $x^2-9\lt 0$ となる $x$ の値の範囲で $x$ の係数が正の1次関数になっているよ。
- 逆に $x^2-9\gt 0$ となる $x$ の値の範囲では、 $x^2$ の係数が負の2次関数になっているよ。
- それらを合わせると、②の関数のグラフは、真ん中が右上がりの直線の一部、両側が上に凸の放物線の一部になっているよ。
- このように考えていけば、あまり計算しなくても、おおよその形は簡単にわかるね。
関数 $y=-\dfrac{1}{8}|x^2-9|-\dfrac{1}{8}x^2+x$ のグラフは $\dBox{ケ}$ である。
次のグラフについても考えてみよう。
・関数 $y=\dfrac{1}{8}|x^2-9|-\dfrac{1}{8}x^2+x$ のグラフは $\dBox{コ}$ である。
・関数 $y=\dfrac{1}{8}|x^2+2\sqrt{5}x-4|+\dfrac{1}{8}(x^2+2\sqrt{5}x)$ のグラフは $\dBox{サ}$ である。
$\dbox{ケ}$ ~ $\dbox{サ}$ については、最も適当なものを次の 0 ~ 9 のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。なお、 $x$ 軸と $y$ 軸は省略してあるが、 $x$ 軸は右方向、 $y$ 軸は上方向がそれぞれ正の方向である。
考え方
グラフの概形を考える問題です。絶対値が入っていて、ちゃんとグラフをかくのは大変だけど、式の形が"良い"場合には、概形を簡単に出すことができます。
絶対値をとって整理したあとの式の形を利用してグラフを選びましょう。
【必答問題】
解答編
問題
花子さんと太郎さんは、絶対値を含む関数のグラフについて考えている。
(1) 関数\[ y=\frac{1}{8}|x^2+2x-8|+\frac{1}{8}(x^2-6x) \quad \cdots ① \]のグラフを考える。
(i) 2次不等式 $x^2+2x-8\lt 0$ の解は $\myBox{アイ}\lt x\lt\myBox{ウ}$ である。
$\mybox{アイ}\lt x\lt\mybox{ウ}$ のとき、 $x^2+2x-8$ の値は負となるので、①は\[ y=-\frac{1}{8}(x^2+2x-8)+\frac{1}{8}(x^2-6x)=-x+1 \]と変形できる。
$x\leqq \mybox{アイ}$, $\mybox{ウ}\leqq x$ のとき、①は\[ y=\frac{1}{8}(x^2+2x-8)+\frac{1}{8}(x^2-6x)=\frac{1}{4}x^2-\frac{1}{2}x-1 \]と変形できる。
解説
(1)(i)
$x^2+2x-8=(x+4)(x-2)$ なので、 $x^2+2x-8\lt 0$ の解は $-4\lt x\lt 2$ となります。
解答
アイウ:-42 (2点)
解答編 つづき
問題
(ii) 2次関数\[ y=\frac{1}{4}x^2-\frac{1}{2}x-1 \]のグラフの頂点の座標は $\left(\myBox{エ},\dfrac{\myBox{オカ}}{\myBox{キ}}\right)$ である。
解説
(1)(ii)
\begin{eqnarray}
y &=& \frac{1}{4}x^2-\frac{1}{2}x-1 \\[5pt]
&=& \frac{1}{4}(x^2-2x)-1 \\[5pt]
&=& \frac{1}{4}\{(x-1)^2-1\}-1 \\[5pt]
&=& \frac{1}{4}(x-1)^2-\frac{5}{4} \\[5pt]
\end{eqnarray}なので、頂点の座標は $\left(1,\dfrac{-5}{4}\right)$ となります。
解答
エオカキ:1-54 (3点)
解答編 つづき
問題
(iii) ①のグラフは $\dBox{ク}$ である。
$\dbox{ク}$ については、最も適当なものを次の 0 ~ 9 のうちから一つ選べ。なお、 $x$ 軸と $y$ 軸は省略してあるが、 $x$ 軸は右方向、 $y$ 軸は上方向がそれぞれ正の方向である。
解説
(1)(iii)
まず、 $-4\lt x\lt 2$ の範囲では、 $y=-x+1$ なので、右下がりの直線だから、この時点で 1 か 4 にしぼることができます。さらに、これ以外の範囲では、 $x^2$ の係数が正の二次関数のグラフになるので、 1 だとわかります。
解答
ク:1 (3点)
解答編 つづき
問題
(2) 花子さんと太郎さんは、(1)を振り返って、グラフのおおよその形をより簡単に知る手順を、関数\[ y=-\frac{1}{8}|x^2-9|-\frac{1}{8}x^2+x \quad \cdots ② \]を例にして考えている。
- ①の関数のグラフを考えるのは大変だったね。おおよその形でよいから、あまり計算せずに簡単に知ることはできないかな。
- ②の関数も①の関数と同じように $x^2$ の項が消えて1次関数となるような $x$ の値の範囲があるね。具体的には、 $x^2-9\lt 0$ となる $x$ の値の範囲で $x$ の係数が正の1次関数になっているよ。
- 逆に $x^2-9\gt 0$ となる $x$ の値の範囲では、 $x^2$ の係数が負の2次関数になっているよ。
- それらを合わせると、②の関数のグラフは、真ん中が右上がりの直線の一部、両側が上に凸の放物線の一部になっているよ。
- このように考えていけば、あまり計算しなくても、おおよその形は簡単にわかるね。
関数 $y=-\dfrac{1}{8}|x^2-9|-\dfrac{1}{8}x^2+x$ のグラフは $\dBox{ケ}$ である。
次のグラフについても考えてみよう。
・関数 $y=\dfrac{1}{8}|x^2-9|-\dfrac{1}{8}x^2+x$ のグラフは $\dBox{コ}$ である。
・関数 $y=\dfrac{1}{8}|x^2+2\sqrt{5}x-4|+\dfrac{1}{8}(x^2+2\sqrt{5}x)$ のグラフは $\dBox{サ}$ である。
$\dbox{ケ}$ ~ $\dbox{サ}$ については、最も適当なものを次の 0 ~ 9 のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。なお、 $x$ 軸と $y$ 軸は省略してあるが、 $x$ 軸は右方向、 $y$ 軸は上方向がそれぞれ正の方向である。
解説
(2)
$y=-\dfrac{1}{8}|x^2-9|-\dfrac{1}{8}x^2+x$ のグラフは、会話にもあるように、 $x^2\lt 9$ の範囲、つまり、 $-3\lt x\lt 3$ の範囲では絶対値の中が負となり、1次関数のグラフになります。 $x$ の係数は $1$ で正だから、右上がりの直線です。なので、 0 か 3 のグラフです。一方、絶対値の中が正のときは、右辺は $x^2$ の係数が負の2次関数なので、グラフは上に凸だから、 3 のグラフとなります。
$y=\dfrac{1}{8}|x^2-9|-\dfrac{1}{8}x^2+x$ は、絶対値の中が正の場合、つまり、 $x\gt 3$ または $x\lt -3$ の場合に $x^2$ の項が消えます。 $x$ の係数が正の1次関数のグラフだから、右上がりの直線なので、6 か 8 のグラフです。一方、絶対値の中が負の場合、右辺は $x^2$ の係数が負なので、上に凸のグラフだから、8 のグラフとなります。
$y=\dfrac{1}{8}|x^2+2\sqrt{5}x-4|+\dfrac{1}{8}(x^2+2\sqrt{5}x)$ は、絶対値の中が負の場合、右辺は定数になります。絶対値の中の2次関数は、判別式が正なので、 $a\lt x\lt b$ のような形の区間で、 $x$ 軸に平行な直線になることがわかります。なので、2 か 5 のグラフとなります。絶対値の中が正のときは、右辺の $x^2$ の係数は正なので、下に凸のグラフだから、2 のグラフとなります。
解答
ケ:3 (2点)
コ:8 (2点)
サ:2 (3点)