共通テスト 数学I・数学A 2024年度追試 第1問 [3] 解説
【必答問題】
問題編
問題
三角形に関連する量と三角形の合同条件について考察する。
(1) $\triangle\mathrm{ABC}$ において、 $\mathrm{BC}=4$ であり、 $\triangle \mathrm{ABC}$ の外接円の半径は $\dfrac{4\sqrt{3}}{3}$ であるとする。このとき、 $\angle\mathrm{BAC}$ の大きさについて二つの場合を考えることができ、そのうちの小さい方は $\dBox{テ}$ であり、大きい方は $\dBox{ト}$ である。さらに、 $\triangle \mathrm{ABC}$ の面積は $\dfrac{3\sqrt{3}}{4}$ であるとする。このとき、 $\mathrm{AB\cdot AC}=\myBox{ナ}$ である。
$\angle \mathrm{BAC}=\dbox{テ}$ のとき、余弦定理より $\mathrm{AB^2+AC^2}=\myBox{ニヌ}$ なので $(\mathrm{AB+AC})^2=\myBox{ネノ}$ である。よって、 $\mathrm{AC}=\myBox{ハ}-\mathrm{AB}$ より\[ \mathrm{AB}=\frac{\myBox{ヒ}\pm\sqrt{\myBox{フヘ}}}{2} \]である。
また、 $\angle\mathrm{BAC}=\dbox{ト}$ のとき、同様に考えると、 $\mathrm{AB} = \dfrac{\sqrt{19}\pm\sqrt{7}}{2}$ であることがわかる。
$\dbox{テ},\ \dbox{ト}$ の解答群
0: $30^{\circ}$
1: $45^{\circ}$
2: $60^{\circ}$
3: $90^{\circ}$
4: $120^{\circ}$
5: $135^{\circ}$
6: $150^{\circ}$(2) 次の命題(a), (b)の真偽の組合せとして正しいものは $\dBox{ホ}$ である。
(a) 二つの三角形において、一組の辺、面積、外接円の半径がそれぞれ等しいならば、その二つの三角形は合同である。
(b) 二つの三角形において、一組の角、面積、外接円の半径がそれぞれ等しいならば、その二つの三角形は合同である。
$\dbox{ホ}$ の解答群
0: (a)真 (b)真
1: (a)真 (b)偽
2: (a)偽 (b)真
3: (a)偽 (b)偽
考え方
面積から辺の積を求めるなど、前半はあまり見ないタイプの計算があります。後半は、前半の結果をどう使うかが少しわかりづらく、両方とも正しく答えるのはなかなか難しいです。まずは、前半のケースが、どちらのケースの何に(証明か、反例か)対応するのかを考えましょう。
図をかいて考えるのもやりづらいです。そもそも、問題全体で何をやっているかを理解するのも大変でしょう。
【必答問題】
解答編
問題
三角形に関連する量と三角形の合同条件について考察する。
(1) $\triangle\mathrm{ABC}$ において、 $\mathrm{BC}=4$ であり、 $\triangle \mathrm{ABC}$ の外接円の半径は $\dfrac{4\sqrt{3}}{3}$ であるとする。このとき、 $\angle\mathrm{BAC}$ の大きさについて二つの場合を考えることができ、そのうちの小さい方は $\dBox{テ}$ であり、大きい方は $\dBox{ト}$ である。さらに、 $\triangle \mathrm{ABC}$ の面積は $\dfrac{3\sqrt{3}}{4}$ であるとする。このとき、 $\mathrm{AB\cdot AC}=\myBox{ナ}$ である。
$\angle \mathrm{BAC}=\dbox{テ}$ のとき、余弦定理より $\mathrm{AB^2+AC^2}=\myBox{ニヌ}$ なので $(\mathrm{AB+AC})^2=\myBox{ネノ}$ である。よって、 $\mathrm{AC}=\myBox{ハ}-\mathrm{AB}$ より\[ \mathrm{AB}=\frac{\myBox{ヒ}\pm\sqrt{\myBox{フヘ}}}{2} \]である。
また、 $\angle\mathrm{BAC}=\dbox{ト}$ のとき、同様に考えると、 $\mathrm{AB} = \dfrac{\sqrt{19}\pm\sqrt{7}}{2}$ であることがわかる。
$\dbox{テ},\ \dbox{ト}$ の解答群
0: $30^{\circ}$
1: $45^{\circ}$
2: $60^{\circ}$
3: $90^{\circ}$
4: $120^{\circ}$
5: $135^{\circ}$
6: $150^{\circ}$
解説
(1)
外接円の半径を $R$ とすると、正弦定理より、
\begin{eqnarray}
\frac{\mathrm{BC}}{\sin\angle\mathrm{BAC}} &=& 2R \\[5pt]
4 &=& 2 \cdot \frac{4\sqrt{3}}{3} \cdot \sin\angle\mathrm{BAC} \\[5pt]
\sin\angle\mathrm{BAC} &=& \frac{\sqrt{3}}{2} \\[5pt]
\end{eqnarray}なので、$\angle\mathrm{BAC}$ は $60^{\circ}, 120^{\circ}$ となります。
面積は $\dfrac{1}{2}\mathrm{AB\cdot AC}\sin\angle\mathrm{BAC}$ で表されるので
\begin{eqnarray}
\dfrac{1}{2}\mathrm{AB\cdot AC}\sin\angle\mathrm{BAC} &=& \frac{3\sqrt{3}}{4} \\[5pt]
\mathrm{AB\cdot AC}\cdot\frac{\sqrt{3}}{2} &=& \frac{3\sqrt{3}}{2} \\[5pt]
\mathrm{AB\cdot AC} &=& 3 \\[5pt]
\end{eqnarray}と求められます。
$\angle\mathrm{BAC}=60^{\circ}$ のとき、余弦定理より
\begin{eqnarray}
& & \mathrm{BC}^2=\mathrm{AB}^2+\mathrm{AC}^2-2\mathrm{AB}\cdot\mathrm{AC}\cos\angle\mathrm{BAC} \\[5pt]
& & 4^2=\mathrm{AB}^2+\mathrm{AC}^2-2\cdot 3 \cos60^{\circ} \\[5pt]
& & 16=\mathrm{AB}^2+\mathrm{AC}^2-3 \\[5pt]
& & \mathrm{AB}^2+\mathrm{AC}^2=19 \\[5pt]
\end{eqnarray}
なので
\begin{eqnarray}
& & \mathrm{AB}^2+\mathrm{AC}^2=19 \\[5pt]
& & \mathrm{AB}^2+2\mathrm{AB}\cdot\mathrm{AC}+\mathrm{AC}^2=19+2\mathrm{AB}\cdot\mathrm{AC} \\[5pt]
& & (\mathrm{AB}+\mathrm{AC})^2=19+2\cdot3=25 \\[5pt]
\end{eqnarray}だから、 $\mathrm{AC}=5-\mathrm{AB}$ となります。これを ナ のところに代入すると
\begin{eqnarray}
\mathrm{AB}\cdot\mathrm{AC} &=& 3 \\[5pt]
\mathrm{AB}\cdot(5-\mathrm{AB}) &=& 3 \\[5pt]
\mathrm{AB}^2-5\mathrm{AB}+3 &=& 0 \\[5pt]
\mathrm{AB} &=& \frac{5\pm\sqrt{5^2-4\cdot 3}}{2} \\[5pt]
&=& \frac{5\pm\sqrt{13}}{2} \\[5pt]
\end{eqnarray}と求められます。
また、問題文には $\angle\mathrm{BAC}=120^{\circ}$ のときも結果だけ書かれていますが、一応この結果も確認しておきます。余弦定理より、
\begin{eqnarray}
& & \mathrm{BC}^2=\mathrm{AB}^2+\mathrm{AC}^2-2\mathrm{AB}\cdot\mathrm{AC}\cos\angle\mathrm{BAC} \\[5pt]
& & 4^2=\mathrm{AB}^2+\mathrm{AC}^2-2\cdot 3 \cos120^{\circ} \\[5pt]
& & 16=\mathrm{AB}^2+\mathrm{AC}^2+3 \\[5pt]
& & \mathrm{AB}^2+\mathrm{AC}^2=13 \\[5pt]
\end{eqnarray}
なので
\begin{eqnarray}
& & \mathrm{AB}^2+\mathrm{AC}^2=13 \\[5pt]
& & \mathrm{AB}^2+2\mathrm{AB}\cdot\mathrm{AC}+\mathrm{AC}^2=13+2\mathrm{AB}\cdot\mathrm{AC} \\[5pt]
& & (\mathrm{AB}+\mathrm{AC})^2=13+2\cdot3=19 \\[5pt]
\end{eqnarray}
だから、 $\mathrm{AC}=\sqrt{19}-\mathrm{AB}$ となります。これを ナ のところに代入すると
\begin{eqnarray}
\mathrm{AB}\cdot\mathrm{AC} &=& 3 \\[5pt]
\mathrm{AB}\cdot(\sqrt{19}-\mathrm{AB}) &=& 3 \\[5pt]
\mathrm{AB}^2-\sqrt{19}\mathrm{AB}+3 &=& 0 \\[5pt]
\mathrm{AB} &=& \frac{\sqrt{19}\pm\sqrt{19-4\cdot 3}}{2} \\[5pt]
&=& \frac{\sqrt{19}\pm\sqrt{7}}{2} \\[5pt]
\end{eqnarray}となり、たしかに問題文の通りだとわかります。
解答
テト:24 (3点)
ナ:3 (2点)
ニヌ:19 (2点)
ネノハ:255 (2点)
ヒフヘ:513 (3点)
解答編 つづき
問題
(2) 次の命題(a), (b)の真偽の組合せとして正しいものは $\dBox{ホ}$ である。
(a) 二つの三角形において、一組の辺、面積、外接円の半径がそれぞれ等しいならば、その二つの三角形は合同である。
(b) 二つの三角形において、一組の角、面積、外接円の半径がそれぞれ等しいならば、その二つの三角形は合同である。
$\dbox{ホ}$ の解答群
0: (a)真 (b)真
1: (a)真 (b)偽
2: (a)偽 (b)真
3: (a)偽 (b)偽
解説
(2)
まず、(a)についてですが、これは(1)が利用できます。
$\triangle\mathrm{ABC}, \triangle\mathrm{DEF}$ について、 $\mathrm{AB}=\dfrac{5+\sqrt{13}}{2}$, $\mathrm{BC}=4$, $\mathrm{CA}=\dfrac{5-\sqrt{13}}{2}$ であり、 $\mathrm{DE}=\dfrac{\sqrt{19}+\sqrt{7}}{2}$, $\mathrm{EF}=4$, $\mathrm{FD}=\dfrac{\sqrt{19}-\sqrt{7}}{2}$ とします。これは、(1)で出てきた2つの三角形です。
このとき、 $\mathrm{BC=EF}=4$ であり、面積はどちらも $\dfrac{3\sqrt{3}}{4}$ であり、外接円の半径はどちらも $\dfrac{4\sqrt{3}}{3}$ ですが、この2つの三角形は合同ではありません。なので、(a)は偽であることがわかります。
次に、(b)について考えます。
$\triangle\mathrm{ABC}, \triangle\mathrm{DEF}$ について、一組の角が等しいとします。 $\angle\mathrm{BAC}=\angle\mathrm{DEF}$ としてもかまいません。正弦定理と外接円の半径が等しいことから、 $\mathrm{BC}=\mathrm{DF}$ が言えます。面積が等しいので、(1)と同じようにして、 $\mathrm{AB\cdot AC}=\mathrm{DE\cdot DF}$ が言えます。また、(1)のように余弦定理を使えば、\[ \mathrm{AB+AC}=\mathrm{DE+DF} \]も言えます。和と積が同じなら、2つの値の組は同じなので、$\triangle\mathrm{ABC}$ と $\triangle\mathrm{DEF}$ が合同であることが言えます。なので、(b)は真であることがわかります。
ところで、これは何をやっているのでしょうか。計算だけだとわかりにくいですが、図形でも考えてみます。
辺を1つ固定して、円も固定します。
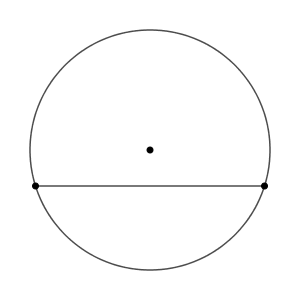
面積も決まっているとすると、高さが決まってしまいます。ただ、この辺からある距離だけ離れた直線は、次のように2本引ける場合があります。
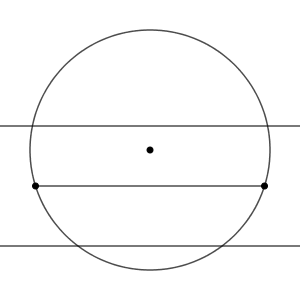
これを利用して、次のような2つの三角形を考えてみます。

この場合、1組の辺が等しく、外接円の半径も面積も等しいですが、合同ではない、という2つの三角形がかけてしまいます。
一方、角を1つ決めた場合を考えます。正弦定理から対辺の長さが決まります。先ほどと同じように円を固定します。

面積も決まっているなら高さが決まりますが、今回は角を決めているので、先ほどとは異なり、鈍角か鋭角かに応じて、どちらの直線を使うかが決まってしまいます。そのため、三角形の形も大きさも決まってしまいます。
解答
ホ:2 (3点)





