共通テスト数学I・数学A 2024年度追試第1問 [2] 解説

🕒 2024/02/25

【必答問題】

問題編

問題

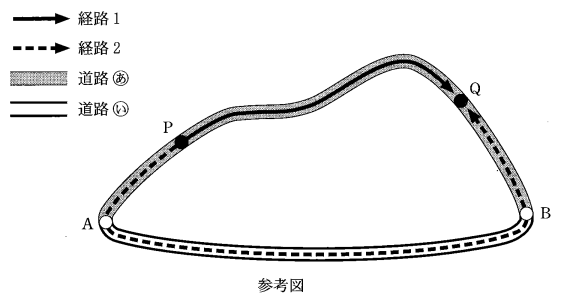
　地点Aと地点Bが一般道路$\bigcirc \llap{\text{あ}}$ （以下、道路$\bigcirc \llap{\text{あ}}$ ）と高速道路$\bigcirc \llap{\text{い}}$ （以下、道路$\bigcirc \llap{\text{い}}$ ）でつながっている。車の制限速度は、道路$\bigcirc \llap{\text{あ}}$ が時速 $30\mathrm{km}$ で、道路$\bigcirc \llap{\text{い}}$ が時速 $80\mathrm{km}$ である。道路$\bigcirc \llap{\text{あ}}$ におけるAからBまでの道のりは $75\mathrm{km}$ であり、道路$\bigcirc \llap{\text{い}}$ におけるAからBまでの道のりは $48\mathrm{km}$ である。

　道路$\bigcirc \llap{\text{あ}}$ 上に地点Pがあり、道路$\bigcirc \llap{\text{あ}}$ におけるPからAまでの道のりは $10\mathrm{km}$ である。また、地点Qは道路$\bigcirc \llap{\text{あ}}$ においてPとBの間にある。ただし、Qは、P, Bのいずれとも異なる地点である。

　太郎さんは、PからQに車で行くことになった。PからQに行くには、Pから道路$\bigcirc \llap{\text{あ}}$ だけを通ってQに行く経路１と、Pから道路$\bigcirc \llap{\text{あ}}$ を通ってAに行き、Aから道路$\bigcirc \llap{\text{い}}$ を通ってBに行き、Bから道路$\bigcirc \llap{\text{あ}}$ を通ってQに行く経路２がある。

　道路$\bigcirc \llap{\text{あ}}$ におけるPからQまでの道のりがどれくらいであれば、経路２を選ぶ方が経路１を選ぶよりも短い時間でQに到着できるかを考えたい。ただし、車はつねに制限速度で走るものとする。

　道路$\bigcirc \llap{\text{あ}}$ において、PからQまでの道のりを $x\mathrm{km}$ とすると、PからAまでの道のりが $10\mathrm{km}$ であり、PとBの間にQがあることから、 $x\lt 65$ である。

　経路２を選ぶとき、道路$\bigcirc \llap{\text{あ}}$ を通っている時間は $\dfrac{\myBox{キク}-x}{\myBox{ケコ}}$ 時間となるので、経路２を選んだ場合のPからQまでの所要時間は $\left(\dfrac{\mybox{キク}-x}{\mybox{ケコ}}+\dfrac{\myBox{サ}}{\myBox{シ}}\right)$ 時間となる。よって、経路２を選ぶ方が経路１を選ぶより短い時間でQに到着できることを表す不等式は\[ \left(\dfrac{\mybox{キク}-x}{\mybox{ケコ}}+\dfrac{\mybox{サ}}{\mybox{シ}}\right) \dBox{ス} \frac{x}{\myBox{セソ}} \]となる。これを解くと、\[ x\gt \myBox{タチ}.\ \myBox{ツ} \]となる。したがって、道路$\bigcirc \llap{\text{あ}}$ におけるPからQまでの道のりが $\mybox{タチ}.\ \mybox{ツ}\mathrm{km}$ より長ければ、経路２を選ぶ方が経路１を選ぶより短い時間でQに到着することができる。

　$\dbox{ス}$ の解答群

　0: $\lt$
　1: $\gt$

考え方

一次不等式の問題です。問題文が長いですが、2つの経路の距離、時間を求めて比較しているだけです。

【必答問題】

解答編

問題

　地点Aと地点Bが一般道路$\bigcirc \llap{\text{あ}}$ （以下、道路$\bigcirc \llap{\text{あ}}$ ）と高速道路$\bigcirc \llap{\text{い}}$ （以下、道路$\bigcirc \llap{\text{い}}$ ）でつながっている。車の制限速度は、道路$\bigcirc \llap{\text{あ}}$ が時速 $30\mathrm{km}$ で、道路$\bigcirc \llap{\text{い}}$ が時速 $80\mathrm{km}$ である。道路$\bigcirc \llap{\text{あ}}$ におけるAからBまでの道のりは $75\mathrm{km}$ であり、道路$\bigcirc \llap{\text{い}}$ におけるAからBまでの道のりは $48\mathrm{km}$ である。

　道路$\bigcirc \llap{\text{あ}}$ 上に地点Pがあり、道路$\bigcirc \llap{\text{あ}}$ におけるPからAまでの道のりは $10\mathrm{km}$ である。また、地点Qは道路$\bigcirc \llap{\text{あ}}$ においてPとBの間にある。ただし、Qは、P, Bのいずれとも異なる地点である。

　太郎さんは、PからQに車で行くことになった。PからQに行くには、Pから道路$\bigcirc \llap{\text{あ}}$ だけを通ってQに行く経路１と、Pから道路$\bigcirc \llap{\text{あ}}$ を通ってAに行き、Aから道路$\bigcirc \llap{\text{い}}$ を通ってBに行き、Bから道路$\bigcirc \llap{\text{あ}}$ を通ってQに行く経路２がある。

　道路$\bigcirc \llap{\text{あ}}$ におけるPからQまでの道のりがどれくらいであれば、経路２を選ぶ方が経路１を選ぶよりも短い時間でQに到着できるかを考えたい。ただし、車はつねに制限速度で走るものとする。

　道路$\bigcirc \llap{\text{あ}}$ において、PからQまでの道のりを $x\mathrm{km}$ とすると、PからAまでの道のりが $10\mathrm{km}$ であり、PとBの間にQがあることから、 $x\lt 65$ である。

　経路２を選ぶとき、道路$\bigcirc \llap{\text{あ}}$ を通っている時間は $\dfrac{\myBox{キク}-x}{\myBox{ケコ}}$ 時間となるので、経路２を選んだ場合のPからQまでの所要時間は $\left(\dfrac{\mybox{キク}-x}{\mybox{ケコ}}+\dfrac{\myBox{サ}}{\myBox{シ}}\right)$ 時間となる。よって、経路２を選ぶ方が経路１を選ぶより短い時間でQに到着できることを表す不等式は\[ \left(\dfrac{\mybox{キク}-x}{\mybox{ケコ}}+\dfrac{\mybox{サ}}{\mybox{シ}}\right) \dBox{ス} \frac{x}{\myBox{セソ}} \]となる。

　$\dbox{ス}$ の解答群

　0: $\lt$
　1: $\gt$

解説

経路２を選ぶとき、道路あを通る長さは、道路あからP・Q間を除いた部分なので、 $75-x\mathrm{km}$ となります。なので、この部分を時速 $30\mathrm{km}$ で走るので、道路あを通っている時間は\[ \frac{75-x}{30} \]時間となります。道路いを通っている時間は $\dfrac{48}{80}$ 時間なので、経路２を選んだ時のPからQまでの所要時間は\[ \frac{75-x}{30}+\frac{48}{80}=\frac{75-x}{30}+\frac{3}{5} \]となります。経路１を選んだ場合の所要時間は $\dfrac{x}{30}$ なので、経路２の方が短い時間でQに到着できることを表す不等式は\[ \frac{75-x}{30}+\frac{3}{5} \lt \dfrac{x}{30} \]となります。不等号の向きを考えるときには、問題文にある式の左辺が経路2に対応することに注意しましょう。

解答

キクケコ：7530 (2点)
サシ：35 (2点)
スセソ：030 (2点)

解答編　つづき

問題

これを解くと、\[ x\gt \myBox{タチ}.\ \myBox{ツ} \]となる。したがって、道路$\bigcirc \llap{\text{あ}}$ におけるPからQまでの道のりが $\mybox{タチ}.\ \mybox{ツ}\mathrm{km}$ より長ければ、経路２を選ぶ方が経路１を選ぶより短い時間でQに到着することができる。

解説

この不等式を解くと
\begin{eqnarray} \frac{75-x}{30}+\frac{3}{5} & \lt & \dfrac{x}{30} \\[5pt] (75-x)+3\cdot 6 & \lt & x \\[5pt] -2x & \lt & -93 \\[5pt] x & \gt & 46.5 \\[5pt] \end{eqnarray}なので、P・Q間が$46.5\mathrm{km}$ より長ければ、経路２を選んだ方がはやく到着できることがわかります。