共通テスト数学I・数学A 2023年度第4問解説

🕒 2023/01/15 🔄 2023/05/01

【第3問～第5問から2問選択】

問題編

問題

　色のついた長方形を並べて正方形や長方形を作ることを考える。色のついた長方形は、向きを変えずにすき間なく並べることとし、色のついた長方形は十分あるものとする。

(1) 横の長さが $462$ で縦の長さが $110$ である赤い長方形を、図１のように並べて正方形や長方形を作ることを考える。

　$462$ と $110$ の両方を割り切る素数のうち最大のものは $\myBox{アイ}$ である。

　赤い長方形を並べて作ることができる正方形のうち、辺の長さが最小であるものは、一辺の長さが $\myBox{ウエオカ}$ のものである。

　また、赤い長方形を並べて正方形ではない長方形を作るとき、横の長さと縦の長さの差の絶対値が最小になるのは、 $462$ の約数と $110$ の約数を考えると、差の絶対値が $\myBox{キク}$ になるときであることがわかる。

　縦の長さが横の長さより $\mybox{キク}$ 長い長方形のうち、横の長さが最小であるものは、横の長さが $\myBox{ケコサシ}$ のものである。

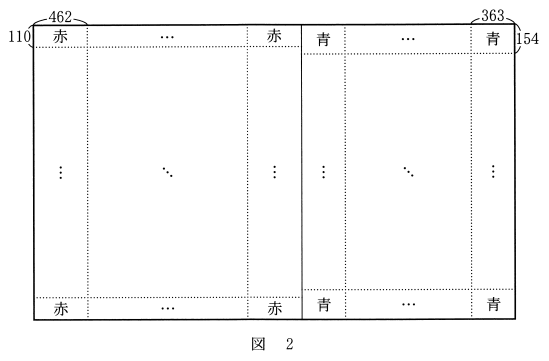
(2) 花子さんと太郎さんは、(1)で用いた赤い長方形を1枚以上並べて長方形を作り、その右側に横の長さが $363$ で縦の長さが $154$ である青い長方形を1枚以上並べて、図２のような正方形や長方形を作ることを考えている。

　このとき、赤い長方形を並べてできる長方形の縦の長さと、青い長方形を並べてできる長方形の縦の長さは等しい。よって、図２のような長方形のうち、縦の長さが最小のものは、縦の長さが $\myBox{スセソ}$ のものであり、図２のような長方形は縦の長さが $\mybox{スセソ}$ の倍数である。

　二人は、次のように話している。

赤い長方形と青い長方形を図２のように並べて正方形を作ってみようよ。

赤い長方形の横の長さが $462$ で青い長方形の横の長さが $363$ だから、図２のような正方形の横の長さは $462$ と $363$ を組み合わせて作ることができる長さでないといけないね。

正方形だから、横の長さは $\mybox{スセソ}$ の倍数でもないといけないね。

　$462$ と $363$ の最大公約数は $\myBox{タチ}$ であり、 $\mybox{タチ}$ の倍数のうちで $\mybox{スセソ}$ の倍数でもある最小の正の整数は $\myBox{ツテトナ}$ である。

　これらのことと、使う長方形の枚数が赤い長方形も青い長方形も1枚以上であることから、図２の正方形のうち、辺の長さが最小であるものは、一辺の長さが $\myBox{ニヌネノ}$ のものであることがわかる。

考え方

問われ方は目新しいですが、やっている内容はよくある最大公約数や不定方程式です。大きな数字が出てきますが、計算はそれほど大変ではないでしょう。

最後の問題は解をどう求めるか思いつきにくいかもしれませんが、4桁の倍数で答えが4桁なので、がんばってしぼることもできるでしょう。

解答編

問題

　色のついた長方形を並べて正方形や長方形を作ることを考える。色のついた長方形は、向きを変えずにすき間なく並べることとし、色のついた長方形は十分あるものとする。

(1) 横の長さが $462$ で縦の長さが $110$ である赤い長方形を、図１のように並べて正方形や長方形を作ることを考える。

　$462$ と $110$ の両方を割り切る素数のうち最大のものは $\myBox{アイ}$ である。

　赤い長方形を並べて作ることができる正方形のうち、辺の長さが最小であるものは、一辺の長さが $\myBox{ウエオカ}$ のものである。

　また、赤い長方形を並べて正方形ではない長方形を作るとき、横の長さと縦の長さの差の絶対値が最小になるのは、 $462$ の約数と $110$ の約数を考えると、差の絶対値が $\myBox{キク}$ になるときであることがわかる。

　縦の長さが横の長さより $\mybox{キク}$ 長い長方形のうち、横の長さが最小であるものは、横の長さが $\myBox{ケコサシ}$ のものである。

解説

(1)
$462=4\cdot110+22$ なので、$462$ と $110$ の両方を割り切る素数のうち最大のものは $11$ です。（最大公約数を聞かれてるわけではないので注意）

最大公約数は $22$ であり、最小公倍数は\[ \frac{462\cdot110}{22}=2310 \]なので、最小の正方形の一辺の長さは $2310$ となります。

縦と横の長さの差は、最大公約数である $22$ で割り切れるので、差の絶対値が正の値のうち最小になるのは $22$ のときです。

縦の長さが横の長さより $22$ 長い長方形を考えます。縦と横に使うそれぞれの枚数を $a,b$ とすると\[ 110a-462b=22 \]ということです。これより\[ 5a-21b=1 \]が得られます。こうなるのは、1の位に着目すれば、 $b=4$ のときで、 $a=17$ のときだとわかります。このときの横の長さは、\[ 462\cdot4=1848 \]となります。

解答

アイ：11 (2点)
ウエオカ：2310 (3点)
キク：22 (3点)
ケコサシ：1848 (3点)

解答編　つづき

問題

(2) 花子さんと太郎さんは、(1)で用いた赤い長方形を1枚以上並べて長方形を作り、その右側に横の長さが $363$ で縦の長さが $154$ である青い長方形を1枚以上並べて、図２のような正方形や長方形を作ることを考えている。

　このとき、赤い長方形を並べてできる長方形の縦の長さと、青い長方形を並べてできる長方形の縦の長さは等しい。よって、図２のような長方形のうち、縦の長さが最小のものは、縦の長さが $\myBox{スセソ}$ のものであり、図２のような長方形は縦の長さが $\mybox{スセソ}$ の倍数である。

　二人は、次のように話している。

赤い長方形と青い長方形を図２のように並べて正方形を作ってみようよ。

赤い長方形の横の長さが $462$ で青い長方形の横の長さが $363$ だから、図２のような正方形の横の長さは $462$ と $363$ を組み合わせて作ることができる長さでないといけないね。

正方形だから、横の長さは $\mybox{スセソ}$ の倍数でもないといけないね。

　$462$ と $363$ の最大公約数は $\myBox{タチ}$ であり、 $\mybox{タチ}$ の倍数のうちで $\mybox{スセソ}$ の倍数でもある最小の正の整数は $\myBox{ツテトナ}$ である。

　これらのことと、使う長方形の枚数が赤い長方形も青い長方形も1枚以上であることから、図２の正方形のうち、辺の長さが最小であるものは、一辺の長さが $\myBox{ニヌネノ}$ のものであることがわかる。

解説

(2) 縦の長さは $110$ の倍数であり $154$ の倍数でもあります。 $154=110+44$ なので、 $110$ と $154$ の最大公約数は $22$ だから、最小公倍数は\[ \frac{110\cdot154}{22}=770 \]となります。

$462=363+99$ であり、 $363=3\cdot99+66$ であり、 $66$ と $99$ の最大公約数は $33$ だから、 $462$ と $363$ の最大公約数は $33$ となります。

$33$ の倍数のうち、 $770$ の倍数でもあるものを考えます。 $770=23\cdot 33 +11$ なので、最大公約数は $11$ だから、最小公倍数は\[ \frac{33\cdot770}{11}=2310 \]となります。

横に使う赤の枚数と青の枚数をそれぞれ $a,b$ として、全体の横の長さが $2310k$ になったとしましょう。つまり、\[ 462a+363b=2310k \]ということです。 $33$ で割ると\[ 14a+11b=70k \]となります。 $a,b$ が正の整数で、これを満たし、 $k$ が最小になる場合を考えます。

ここで、\[ 11b=70k-14a=14(5k-2a) \]と変形できるので、 $b$ は $14$ の倍数でないといけません。 $b=14c$ としましょう（$c$ は正の整数）。これを代入すると\[ a+11c=5k \]となります。$a,c$ は正なので、 $k\geqq 3$ です。ここで、 $k=3$ とすると、 $a=4,c=1$ がこの式を満たすので、この場合が最小だとわかります。

つまり、最小の正方形の一辺の長さは\[ 3\cdot2310=6930 \]となります。