共通テスト 数学I・数学A 2023年度 第2問 [2] 解説

【必答問題】

問題編

問題

　太郎さんと花子さんは、バスケットボールのプロ選手の中には、リングと同じ高さでシュートを打てる人がいることを知り、シュートを打つ高さによってボールの軌道がどう変わるかについて考えている。

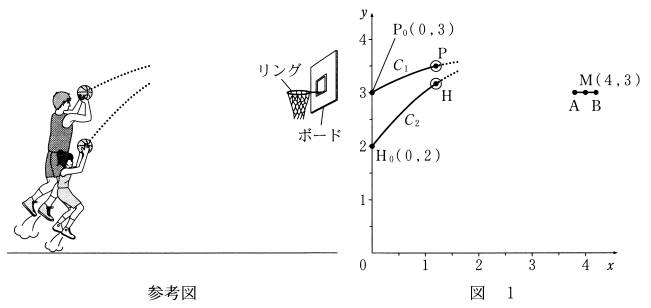
　二人は、図１のように座標軸が定められた平面上に、プロ選手と花子さんがシュートを打つ様子を真横から見た図をかき、ボールがリングに入った場合について、後の仮定を設定して考えることにした。長さの単位はメートルであるが、以下では省略する。

仮定

• 平面上では、ボールを直径 $0.2$ の円とする。
• リングを真横から見たときの左端を点 $\mathrm{A}(3.8,3)$、右端を点 $\mathrm{B}(4.2,3)$ とし、リングの太さは無視する。
• ボールがリングや他のものに当たらずに上からリングを通り、かつ、ボールの中心が $\mathrm{AB}$ の中点 $\mathrm{M}(4,3)$ を通る場合を考える。ただし、ボールがリングに当たるとは、ボールの中心と $\mathrm{A}$ または $\mathrm{B}$ との距離が $0.1$ 以下になることとする。
• プロ選手がシュートを打つ場合のボールの中心を点 $\mathrm{P}$ とし、 $\mathrm{P}$ は、はじめに点 $\mathrm{P}_0(0,3)$ にあるものとする。また、 $\mathrm{P_0, M}$ を通る、上に凸の放物線を $C_1$ とし、 $\mathrm{P}$ は $C_1$ 上を動くものとする。
• 花子さんがシュートを打つ場合のボールの中心を点 $\mathrm{H}$ とし、 $\mathrm{H}$ は、はじめに点 $\mathrm{H_0}(0,2)$ にあるものとする。また、 $\mathrm{H_0,M}$ を通る、上に凸の放物線を $C_2$ とし、 $\mathrm{H}$ は $C_2$ 上を動くものとする。
• 放物線 $C_1$ や $C_2$ に対して、頂点の $y$ 座標を「シュートの高さ」とし、頂点の $x$ 座標を「ボールが最も高くなるときの地上の位置」とする。

(1) 放物線 $C_1$ の方程式における $x^2$ の係数を $a$ とする。放物線 $C_1$ の方程式は\[ y=ax^2-\myBox{キ}ax+\myBox{ク} \]と表すことができる。また、プロ選手の「シュートの高さ」は\[ -\myBox{ケ}a+\myBox{コ} \]である。

　放物線 $C_2$ の方程式における $x^2$ の係数を $p$ とする。放物線 $C_2$ の方程式は\[ y=p\left\{x-\left(2-\frac{1}{8p}\right)\right\}^2-\frac{(16p-1)^2}{64p}+2 \]と表すことができる。

　プロ選手と花子さんの「ボールが最も高くなるときの地上の位置」の比較の記述として、次の 0 ～ 3 のうち、正しいものは $\myBox{サ}$ である。

$\dbox{サ}$ の解答群

　0: プロ選手と花子さんの「ボールが最も高くなるときの地上の位置」は、つねに一致する。

　1: プロ選手の「ボールが最も高くなるときの地上の位置」の方が、つねに $\mathrm{M}$ の $x$ 座標に近い。

　2: 花子さんの「ボールが最も高くなるときの地上の位置」の方が、つねに $\mathrm{M}$ の $x$ 座標に近い。

　3: プロ選手の「ボールが最も高くなるときの地上の位置」の方が $\mathrm{M}$ の $x$ 座標に近いときもあれば、花子さんの「ボールが最も高くなるときの地上の位置」の方が $\mathrm{M}$ の $x$ 座標に近いときもある。

(2) 二人は、ボールがリングすれすれを通る場合のプロ選手と花子さんの「シュートの高さ」について次のように話している。

• 例えば、プロ選手のボールがリングに当たらないようにするには、 $\mathrm{P}$ がリングの左端 $\mathrm{A}$ のどのくらい上を通れば良いのかな。
• $\mathrm{A}$ の真上の点で $\mathrm{P}$ が通る点 $\mathrm{D}$ を、線分 $\mathrm{DM}$ が $\mathrm{A}$ を中心とする半径 $0.1$ の円と接するようにとって考えてみたらどうかな。
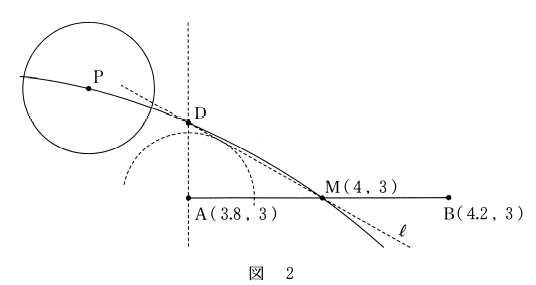
• なるほど。 $\mathrm{P}$ の軌道は上に凸の放物線で山なりだから、その場合、図２のように、 $\mathrm{P}$ は $\mathrm{D}$ を通った後で線分 $\mathrm{DM}$ より上側を通るのでボールはリングに当たらないね。花子さんの場合も、 $\mathrm{H}$ がこの $\mathrm{D}$ を通れば、ボールはリングに当たらないね。
• 放物線 $C_1$ と $C_2$ が $\mathrm{D}$ を通る場合でプロ選手と私の「シュートの高さ」を比べてみようよ。

　図２にように、 $\mathrm{M}$ を通る直線 $\ell$ が、 $\mathrm{A}$ を中心とする半径 $0.1$ の円に直線 $\mathrm{AB}$ の上側で接しているとする。また、 $\mathrm{A}$ を通り直線 $\mathrm{AB}$ に垂直な直線を引き、 $\ell$ との交点を $\mathrm{D}$ とする。このとき、 $\mathrm{AD}=\dfrac{\sqrt{3}}{15}$ である。

　よって、放物線 $C_1$ が $\mathrm{D}$ を通るとき、 $C_1$ の方程式は\[ y=-\dfrac{\myBox{シ}\sqrt{\myBox{ス}}}{\myBox{セソ}} \left(x^2-\mybox{キ}x\right)+\mybox{ク} \]となる。

　また、放物線 $C_2$ が $\mathrm{D}$ を通るとき、(1)で与えられた $C_2$ の方程式を用いると、花子さんの「シュートの高さ」は約 $3.4$ と求められる。

　以上のことから、放物線 $C_1$ と $C_2$ が $\mathrm{D}$ を通るとき、プロ選手と花子さんの「シュートの高さ」を比べると、 $\dBox{タ}$ の「シュートの高さ」の方が大きく、その差はボール $\dBox{チ}$ であり。なお、 $\sqrt{3}=1.7320508\cdots$ である。

$\dbox{タ}$ の解答群
　0: プロ選手
　1: 花子さん

$\dbox{チ}$ については、最も適当なものを、次の 0 ～ 3 のうちから一つ選べ。

　0: 約1個分
　1: 約2個分
　2: 約3個分
　3: 約4個分

考え方

計算が複雑になりすぎるものは問題文に答えを書いてくれているので、そのまま使って考えていきましょう。最後は少し計算が面倒で、あまり二次関数とも関係なくなっています。

【必答問題】

解答編

問題

　太郎さんと花子さんは、バスケットボールのプロ選手の中には、リングと同じ高さでシュートを打てる人がいることを知り、シュートを打つ高さによってボールの軌道がどう変わるかについて考えている。

　二人は、図１のように座標軸が定められた平面上に、プロ選手と花子さんがシュートを打つ様子を真横から見た図をかき、ボールがリングに入った場合について、後の仮定を設定して考えることにした。長さの単位はメートルであるが、以下では省略する。

仮定

• 平面上では、ボールを直径 $0.2$ の円とする。
• リングを真横から見たときの左端を点 $\mathrm{A}(3.8,3)$、右端を点 $\mathrm{B}(4.2,3)$ とし、リングの太さは無視する。
• ボールがリングや他のものに当たらずに上からリングを通り、かつ、ボールの中心が $\mathrm{AB}$ の中点 $\mathrm{M}(4,3)$ を通る場合を考える。ただし、ボールがリングに当たるとは、ボールの中心と $\mathrm{A}$ または $\mathrm{B}$ との距離が $0.1$ 以下になることとする。
• プロ選手がシュートを打つ場合のボールの中心を点 $\mathrm{P}$ とし、 $\mathrm{P}$ は、はじめに点 $\mathrm{P}_0(0,3)$ にあるものとする。また、 $\mathrm{P_0, M}$ を通る、上に凸の放物線を $C_1$ とし、 $\mathrm{P}$ は $C_1$ 上を動くものとする。
• 花子さんがシュートを打つ場合のボールの中心を点 $\mathrm{H}$ とし、 $\mathrm{H}$ は、はじめに点 $\mathrm{H_0}(0,2)$ にあるものとする。また、 $\mathrm{H_0,M}$ を通る、上に凸の放物線を $C_2$ とし、 $\mathrm{H}$ は $C_2$ 上を動くものとする。
• 放物線 $C_1$ や $C_2$ に対して、頂点の $y$ 座標を「シュートの高さ」とし、頂点の $x$ 座標を「ボールが最も高くなるときの地上の位置」とする。

(1) 放物線 $C_1$ の方程式における $x^2$ の係数を $a$ とする。放物線 $C_1$ の方程式は\[ y=ax^2-\myBox{キ}ax+\myBox{ク} \]と表すことができる。また、プロ選手の「シュートの高さ」は\[ -\myBox{ケ}a+\myBox{コ} \]である。

解説

(1)
$(0,3)$ と $(4,3)$ を通るので、放物線 $C_1$ の方程式を $y=ax^2+bx+c$ とおくと、まず、 $c=3$ だとわかります。また、
\begin{eqnarray} 3 &=& 16a+4b+3 \\[5pt] 4b &=& -16a \\[5pt] b &=& -4a \\[5pt] \end{eqnarray}なので、 $C_1$ の方程式は\[ y=ax^2-4ax+3 \]となります。

これを平方完成して
\begin{eqnarray} y &=& ax^2-4ax+3 \\[5pt] &=& a(x^2-4x)+3 \\[5pt] &=& a \left\{(x-2)^2-4\right\}+3 \\[5pt] &=& a (x-2)^2-4a+3 \\[5pt] \end{eqnarray}となるので、シュートの高さは\[ -4a+3 \]となります。

解答

キク：43 (3点)
ケコ：43 (3点)

解答編　つづき

問題

　放物線 $C_2$ の方程式における $x^2$ の係数を $p$ とする。放物線 $C_2$ の方程式は\[ y=p\left\{x-\left(2-\frac{1}{8p}\right)\right\}^2-\frac{(16p-1)^2}{64p}+2 \]と表すことができる。

　プロ選手と花子さんの「ボールが最も高くなるときの地上の位置」の比較の記述として、次の 0 ～ 3 のうち、正しいものは $\myBox{サ}$ である。

$\dbox{サ}$ の解答群

　0: プロ選手と花子さんの「ボールが最も高くなるときの地上の位置」は、つねに一致する。

　1: プロ選手の「ボールが最も高くなるときの地上の位置」の方が、つねに $\mathrm{M}$ の $x$ 座標に近い。

　2: 花子さんの「ボールが最も高くなるときの地上の位置」の方が、つねに $\mathrm{M}$ の $x$ 座標に近い。

　3: プロ選手の「ボールが最も高くなるときの地上の位置」の方が $\mathrm{M}$ の $x$ 座標に近いときもあれば、花子さんの「ボールが最も高くなるときの地上の位置」の方が $\mathrm{M}$ の $x$ 座標に近いときもある。

解説

先ほどの平方完成の式から、 $x=2$ のときに高さが最も高くなることがわかります。

一方、問題文にある放物線 $C_2$ の方程式を見ると、 $x=2-\dfrac{1}{8p}$ のときに最も高くなることがわかります。

放物線は上に凸だから、$p$ は負の値なので、 $2\lt 2-\dfrac{1}{8p}$ となります。なので、「ボールが最も高くなるときの地上位置」が $\mathrm{M}$ に近いのは、花子さんだとわかります。

解答

サ：2 (3点)

解答編　つづき

問題

(2) 二人は、ボールがリングすれすれを通る場合のプロ選手と花子さんの「シュートの高さ」について次のように話している。

• 例えば、プロ選手のボールがリングに当たらないようにするには、 $\mathrm{P}$ がリングの左端 $\mathrm{A}$ のどのくらい上を通れば良いのかな。
• $\mathrm{A}$ の真上の点で $\mathrm{P}$ が通る点 $\mathrm{D}$ を、線分 $\mathrm{DM}$ が $\mathrm{A}$ を中心とする半径 $0.1$ の円と接するようにとって考えてみたらどうかな。
• なるほど。 $\mathrm{P}$ の軌道は上に凸の放物線で山なりだから、その場合、図２のように、 $\mathrm{P}$ は $\mathrm{D}$ を通った後で線分 $\mathrm{DM}$ より上側を通るのでボールはリングに当たらないね。花子さんの場合も、 $\mathrm{H}$ がこの $\mathrm{D}$ を通れば、ボールはリングに当たらないね。
• 放物線 $C_1$ と $C_2$ が $\mathrm{D}$ を通る場合でプロ選手と私の「シュートの高さ」を比べてみようよ。

　図２にように、 $\mathrm{M}$ を通る直線 $\ell$ が、 $\mathrm{A}$ を中心とする半径 $0.1$ の円に直線 $\mathrm{AB}$ の上側で接しているとする。また、 $\mathrm{A}$ を通り直線 $\mathrm{AB}$ に垂直な直線を引き、 $\ell$ との交点を $\mathrm{D}$ とする。このとき、 $\mathrm{AD}=\dfrac{\sqrt{3}}{15}$ である。

　よって、放物線 $C_1$ が $\mathrm{D}$ を通るとき、 $C_1$ の方程式は\[ y=-\dfrac{\myBox{シ}\sqrt{\myBox{ス}}}{\myBox{セソ}} \left(x^2-\mybox{キ}x\right)+\mybox{ク} \]となる。

解説

$x=3.8$ のときに、 $y=3+\dfrac{\sqrt{3}}{15}$ になればいいので、 $C_1$ の方程式 $y=ax^2-4ax+3$ に入れて計算すると
\begin{eqnarray} 3+\dfrac{\sqrt{3}}{15} &=& 3.8^2a-4\cdot a\cdot 3.8+3 \\[5pt] \dfrac{\sqrt{3}}{15} &=& 3.8(3.8a-4a) \\[5pt] \dfrac{\sqrt{3}}{15} &=& -3.8\cdot 0.2a \\[5pt] \dfrac{\sqrt{3}}{3} &=& -3.8a \\[5pt] a &=& -\frac{10}{38} \cdot \dfrac{\sqrt{3}}{3} \\[5pt] &=& -\frac{5\sqrt{3}}{57} \\[5pt] \end{eqnarray}となるので、 $C_1$ の方程式は\[ y=-\frac{5\sqrt{3}}{57}(x^2-4x)+3 \]となります。

解答

シスセソ：5357 (3点)

解答編　つづき

問題

　また、放物線 $C_2$ が $\mathrm{D}$ を通るとき、(1)で与えられた $C_2$ の方程式を用いると、花子さんの「シュートの高さ」は約 $3.4$ と求められる。

　以上のことから、放物線 $C_1$ と $C_2$ が $\mathrm{D}$ を通るとき、プロ選手と花子さんの「シュートの高さ」を比べると、 $\dBox{タ}$ の「シュートの高さ」の方が大きく、その差はボール $\dBox{チ}$ であり。なお、 $\sqrt{3}=1.7320508\cdots$ である。

$\dbox{タ}$ の解答群
　0: プロ選手
　1: 花子さん

$\dbox{チ}$ については、最も適当なものを、次の 0 ～ 3 のうちから一つ選べ。

　0: 約1個分
　1: 約2個分
　2: 約3個分
　3: 約4個分

解説

プロ選手のシュートの高さは $-4a+3$ と表せることから
\begin{eqnarray} & & -4\cdot \left(-\frac{5\sqrt{3}}{57}\right)+3 \\[5pt] &=& \frac{20\sqrt{3}}{57}+3 \end{eqnarray}となります。ここで、\[ \frac{1.71}{57}=0.03 \]であることを使うと \begin{eqnarray} & & \frac{20\sqrt{3}}{57}+3 \\[5pt] &=& \frac{20(1.71+\sqrt{3}-1.71)}{57}+3 \\[5pt] &=& \frac{20\cdot 1.71}{57}+3 +\frac{20(\sqrt{3}-1.71)}{57}\\[5pt] &=& 20\cdot0.03+3 +\frac{20(\sqrt{3}-1.71)}{57}\\[5pt] &=& 3.6 +\frac{20(\sqrt{3}-1.71)}{57}\\[5pt] \end{eqnarray}となります。ここで、後半の項は正で \begin{eqnarray} \frac{20(\sqrt{3}-1.71)}{57} &\lt& \frac{20\cdot 0.025}{57} \\[5pt] &\lt& \frac{0.5}{57} \\[5pt] &\lt& 0.01 \\[5pt] \end{eqnarray}となり、ボールの大きさの直径は $0.2$ なので、これに比べてすごく小さいことがわかります。

以上から、プロ選手のほうがシュートの高さが高く、差はおよそ $3.6-3.4=0.2$ なので、ボール約1個分だとわかります。

解答

タチ：00 (3点)