京都大学 理系 2022年度 第4問 解説
問題編
問題
四面体 OABC が
\begin{eqnarray} & & \mathrm{ OA }=4 \ , \\[5pt] & & \mathrm{ OB=AB=BC }=3 \ , \\[5pt] & & \mathrm{ OC=AC }=2\sqrt{3} \\[5pt] \end{eqnarray}を満たしているとする。 P を辺 BC 上の点とし、 $\triangle \mathrm{ OAP }$ の重心を G とする。このとき、次の各問に答えよ。(1) $\overrightarrow{ \mathrm{ PG } }\perp \overrightarrow{ \mathrm{ OA } }$ を示せ。
(2) P が辺 BC 上を動くとき、 PG の最小値を求めよ。
考え方
(1)はベクトルで出題されていますが、必ずしもベクトルで解く必要はありません。図形的に考えることができるなら、それを利用することもできます。
(2)も、どういうときに最小値をとるのか、図形的な性質を利用したほうが計算量は減るでしょう。
解答編
問題
四面体 OABC が
\begin{eqnarray} & & \mathrm{ OA }=4 \ , \\[5pt] & & \mathrm{ OB=AB=BC }=3 \ , \\[5pt] & & \mathrm{ OC=AC }=2\sqrt{3} \\[5pt] \end{eqnarray}を満たしているとする。 P を辺 BC 上の点とし、 $\triangle \mathrm{ OAP }$ の重心を G とする。このとき、次の各問に答えよ。(1) $\overrightarrow{ \mathrm{ PG } }\perp \overrightarrow{ \mathrm{ OA } }$ を示せ。
(2) P が辺 BC 上を動くとき、 PG の最小値を求めよ。
解答
(1)
辺 OA の中点を M とする。
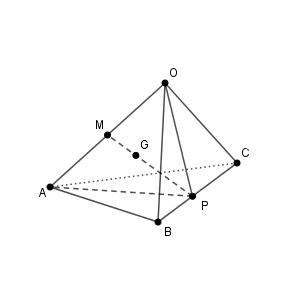
三角形 OBC と三角形 ABC は、3組の辺がそれぞれ等しいので合同。これより、 $\angle \mathrm{ OCP }=\angle \mathrm{ ACP }$ だから、三角形 OCP と三角形 ACP は合同。よって、 $\mathrm{ OP=AP }$ であり、三角形 OAP は二等辺三角形であることがわかる。
これより、 $\mathrm{ OA }\perp \mathrm{ PM }$ であり、 G は PM 上の点なので、$\overrightarrow{ \mathrm{ PG } }\perp \overrightarrow{ \mathrm{ OA } }$ となる、(終)
(2)
$\mathrm{ PG }=\frac{2}{3}\mathrm{ PM }$ なので、 PG が最小となるのは PM が最小となるときである。
三角形 OMP は直角三角形で $\mathrm{ OM }$ の長さは $2$ で固定だから、 PM が最小となるのは OP が最小となるときである。
ここで、 $\angle \mathrm{ OCB }$ は二等辺三角形の底角なので、鋭角である。また、 $\angle \mathrm{ OBC }$ は
\begin{eqnarray}
\cos \angle \mathrm{ OBC }
&=&
\frac{3^2+3^2-(2\sqrt{3})^2}{2\cdot3\cdot 3} \\[5pt]
&=&
\frac{9+9-12}{2\cdot3\cdot 3} \\[5pt]
&\gt&
0
\end{eqnarray}なので、鋭角である。以上から、 OP が最小となるのは、 $\mathrm{ OP }\perp \mathrm{ BC }$ のときだとわかる。
三角形 OBC は、3辺の長さが $3,3,2\sqrt{3}$ の二等辺三角形なので、面積は
\begin{eqnarray}
\frac{2\sqrt{3}\cdot\sqrt{3^2-(\sqrt{3})^2} }{2} =3\sqrt{2}
\end{eqnarray}だから、 BC を底辺としたときの高さは
\begin{eqnarray}
3\sqrt{2}\times2\div 3=2\sqrt{2}
\end{eqnarray}となる。これが OP の最小値なので PM の最小値は
\begin{eqnarray}
\sqrt{ (2\sqrt{2})^2-2^2}=2
\end{eqnarray}となるので、 PG の最小値は $\dfrac{4}{3}$ となる。(答)





