京都大学 理系 2017年度 第5問 解説
問題編
問題
$a\geqq 0$ とする。 $0\leqq x \leqq \sqrt{2}$ の範囲で曲線 $y=xe^{-x}$, 直線 $y=ax$, 直線 $x=\sqrt{2}$ によって囲まれた部分の面積を $S(a)$ とする。このとき、 $S(a)$ の最小値を求めよ。
(ここで「囲まれた部分」とは、上の曲線または直線のうち2つ以上で囲まれた部分を意味するものとする。)
考え方
面積が最小になるのは、2点で交わるときであることはすぐに予想がつきます。積分を計算する必要はありませんが、言及する必要はあります。
2点で交わっているとき、面積を求めるのは少し大変です。やるべきことはすぐにわかりますが、計算は手間取ります。また、それを微分するので、計算はかなり大変です。最小になるときの a を求めるだけなら、 $S(a)$ の積分を計算せずにいきなり微分をすることもできますが、最終的に最小値も求めないといけないので、おとなしく積分するしかありません。
解答編
問題
$a\geqq 0$ とする。 $0\leqq x \leqq \sqrt{2}$ の範囲で曲線 $y=xe^{-x}$, 直線 $y=ax$, 直線 $x=\sqrt{2}$ によって囲まれた部分の面積を $S(a)$ とする。このとき、 $S(a)$ の最小値を求めよ。
(ここで「囲まれた部分」とは、上の曲線または直線のうち2つ以上で囲まれた部分を意味するものとする。)
解説
$f(x)=xe^{-x}$ とすると
\begin{eqnarray}
f'(x)
&=&
e^{-x}-xe^{-x} \\
&=&
e^{-x}(1-x)
\end{eqnarray}なので、 $f'(x)=0$ ならば $x=1$ である。また、 $e^{-x}$ も $(1-x)$ も単調減少なので $f'(x)$ も単調減少であり、 $0\leqq x \leqq \sqrt{2}$ の範囲では $f'(x)\leqq f'(0)=1$ であることもわかる。
$a\geqq 1$ のとき、 $0\leqq x \leqq \sqrt{2}$ の範囲で、
\begin{eqnarray}
ax-xe^{-x}
&=&
x( a-e^{-x} ) \\
&\geqq &
x( 1-e^{0} ) \\
&=&
0
\end{eqnarray}となる。
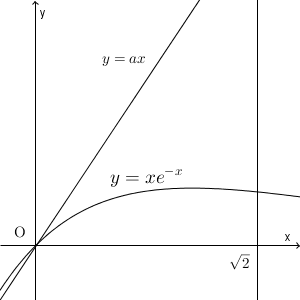
これより、 $0\leqq x \leqq \sqrt{2}$ の範囲では $y=ax$ が $y=f(x)$ より下に来ることはなく、このとき $S(a)$ は単調増加になることがわかる。
また、 $a\leqq e^{-\sqrt{2} }$ のとき、 $0\leqq x \leqq \sqrt{2}$ の範囲で、
\begin{eqnarray}
xe^{-x}-ax
&=&
x( e^{-x}-a ) \\
&\geqq &
x( e^{-x}-e^{-\sqrt{2} } ) \\
&\geqq &
x( e^{-\sqrt{2} }-e^{-\sqrt{2} } ) \\
&=&
0
\end{eqnarray}となる。

これより、 $0\leqq x \leqq \sqrt{2}$ の範囲では $y=ax$ が $y=f(x)$ より上に来ることはなく、このとき $S(a)$ は単調減少になることがわかる。
続いて、 $e^{-\sqrt{2} } \lt a \lt 1$ のときを考える。 $f(x)=ax$ を解くと
\begin{eqnarray}
x( e^{-x}-a )=0
\end{eqnarray}より、 $x=0,-\log a$ となる。今考えている範囲では $0 \lt -\log a \lt \sqrt{2}$ なので、 $0\leqq x \leqq \sqrt{2}$ の範囲で $y=ax$ と $y=f(x)$ の共有点は2点であることがわかる。
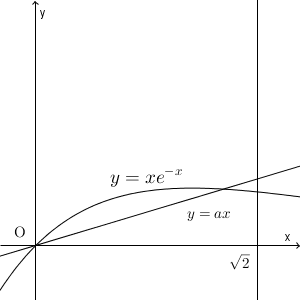
よって、 $S(a)$ は次のように書くことができる。
\begin{eqnarray}
S(a)
&=&
\int_{0}^{-\log a} (xe^{-x}-ax) dx +\int_{-\log a}^{\sqrt{2} } (ax-xe^{-x}) dx \\[5pt]
&=&
\int_{0}^{-\log a} x(e^{-x}-a) dx +\int_{-\log a}^{\sqrt{2} } x(a-e^{-x}) dx \\[5pt]
&=&
\left[ x(-e^{-x}-ax) \right]_{0}^{-\log a} -\int_{0}^{-\log a} (-e^{-x}-ax) dx \\[5pt]
& & +\left[ x(ax+e^{-x}) \right]_{-\log a}^{\sqrt{2} } -\int_{-\log a}^{\sqrt{2} } (ax+e^{-x}) dx \\[5pt]
&=&
(-\log a)(-a+a\log a) -\left[ e^{-x}-\frac{a}{2}x^2 \right]_{0}^{-\log a} \\[5pt]
& & +\sqrt{2}(\sqrt{2}a+e^{-\sqrt{2} }) -(-\log a)(-a\log a+a) \\[5pt]
& & -\left[ \frac{a}{2}x^2-e^{-x} \right]_{-\log a}^{\sqrt{2} } \\[5pt]
&=&
a\log a -a(\log a)^2
-a+\frac{a}{2}(\log a)^2 +1 \\[5pt]
& & +2a+\sqrt{2}e^{-\sqrt{2} } -a(\log a)^2 +a\log a \\[5pt]
& & -\frac{a}{2}\times 2+e^{-\sqrt{2} } +\frac{a}{2}(\log a)^2 -a \\[5pt]
&=&
2a\log a -a(\log a)^2 -a +1 +e^{-\sqrt{2} }(\sqrt{2}+1) \\[5pt]
\end{eqnarray}となる。
この式を a で微分すると
\begin{eqnarray}
S'(a)
&=&
2\log a +2 -(\log a)^2 -a\cdot 2(\log a)\cdot \frac{1}{a} -1 \\[5pt]
&=&
2\log a +1 -(\log a)^2 -2\log a \\[5pt]
&=&
1-(\log a)^2 \\[5pt]
\end{eqnarray}となる。 $S'(a)=0$ とすると $\log a=\pm 1$ となるが、今考えている範囲は $e^{-\sqrt{2} } \lt a \lt 1$ なので、この範囲では $a=e^{-1}$ のみとなる。
以上から、増減表は次のようになる。
\begin{array}{c|ccccc}
a & e^{-\sqrt{2} } & \cdots & e^{-1} & \cdots & 1 \\
\hline
S' & & - & 0 & + & \\
\hline
S & & \searrow & & \nearrow &
\end{array}また、 $a\leqq e^{-\sqrt{2} }$ のときに $S(a)$ は単調減少で、 $a\geqq 1$ のときは単調増加だったから、 $S(a)$ は $a=e^{-1}$ のときに最小値をとることがわかる。この値は
\begin{eqnarray}
S(e^{-1})
&=&
2e^{-1}\cdot(-1) -e^{-1}\cdot(-1)^2 -e^{-1} +1 +e^{-\sqrt{2} }(\sqrt{2}+1) \\[5pt]
&=&
-2e^{-1} -e^{-1} -e^{-1} +1 +e^{-\sqrt{2} }(\sqrt{2}+1) \\[5pt]
&=&
-4e^{-1} +1 +e^{-\sqrt{2} }(\sqrt{2}+1) \\[5pt]
\end{eqnarray}となるので、これが求める最小値である。
(終)
解説
途中の積分は、置換積分をしているのでかなり大変です。もし
\begin{eqnarray}
(-e^{-x}-xe^{-x})'
&=&
e^{-x}-e^{-x}+xe^{-x} \\
&=&
xe^{-x} \\
\end{eqnarray}となることを思いつけば
\begin{eqnarray}
& &
\int_{0}^{-\log a} (xe^{-x}-ax) dx +\int_{-\log a}^{\sqrt{2} } (ax-xe^{-x}) dx \\[5pt]
&=&
\left[ -e^{-x}-xe^{-x}-\frac{a}{2}x^2 \right]_{0}^{-\log a} \\[5pt]
& & +\left[ \frac{a}{2}x^2 +e^{-x}+xe^{-x} \right]_{-\log a}^{\sqrt{2} } \\[5pt]
&=&
-a+a\log a-\frac{a}{2}(\log a)^2 +1 \\[5pt]
& & +\frac{a}{2}\times 2 +e^{-\sqrt{2} }+\sqrt{2}e^{-\sqrt{2} } \\[5pt]
& & -\frac{a}{2}(\log a)^2 -a +a\log a \\[5pt]
&=&
-a+2a\log a-a(\log a)^2 +1 +e^{-\sqrt{2} }(1+\sqrt{2}) \\[5pt]
\end{eqnarray}となり、かなり少しすっきりします。
京大の問題にしては、計算量が多い問題です。





