京都大学 文系 2024年度 第3問 解説
問題編
問題
$a$ は正の整数とする。次の関数の最大値を求めよ。
\begin{eqnarray} f(x) &=& \left|x^2-\left(ax+\frac{3}{4}a^2\right)\right|+ax+\frac{3}{4}a^2 \\[5pt] & & \ (-1\leqq x\leqq 1) \end{eqnarray}
考え方
絶対値が入っていますが、グラフをかくこと自体はそんなに大変ではないです。 $a$ が動くとグラフが動きますが、それによって区間との位置関係が変わってきます。どういうときにどこで最大をとるかを考えて、場合分けをしましょう。
解答編
問題
$a$ は正の整数とする。次の関数の最大値を求めよ。
\begin{eqnarray} f(x) &=& \left|x^2-\left(ax+\frac{3}{4}a^2\right)\right|+ax+\frac{3}{4}a^2 \\[5pt] & & \ (-1\leqq x\leqq 1) \end{eqnarray}
解答
\begin{eqnarray} & & x^2-\left(ax+\frac{3}{4}a^2\right) \\[5pt] &=& x^2-ax-\frac{3}{4}a^2 \\[5pt] &=& \left(x-\frac{3}{2}a\right)\left(x+\frac{1}{2}a\right) \end{eqnarray}であり、 $a\gt 0$ なので、 $-\dfrac{1}{2}a\leqq x\leqq \dfrac{3}{2}a$ のとき $f(x)$ の絶対値の中身は $0$ 以下で、それ以外では正である。よって、 $-\dfrac{1}{2}a\leqq x\leqq \dfrac{3}{2}a$ のとき
\begin{eqnarray}
f(x)
&=&
-x^2+ax+\frac{3}{4}a^2+ax+\frac{3}{4}a^2 \\[5pt]
&=&
-x^2+2ax+\frac{3}{2}a^2 \\[5pt]
&=&
-(x-a)^2+\frac{5}{2}a^2 \\[5pt]
\end{eqnarray}であり、 $x\lt-\dfrac{1}{2}a$ または $x\gt \dfrac{3}{2}a$ のときは
\begin{eqnarray}
f(x)
&=&
x^2-ax-\frac{3}{4}a^2+ax+\frac{3}{4}a^2 \\[5pt]
&=&
x^2
\end{eqnarray}となる。ここで、 $f_1(x)=-(x-a)^2+\dfrac{5}{2}a^2$, $f_2(x)=x^2$ とおく。
また、 $y=f_1(x)$ の最大値 $\dfrac{5}{2}a^2$ と $f_2(x)=x^2$ が等しくなるのは、 $x=\pm\dfrac{\sqrt{10}}{2}$ のときである。
以上から、 $f(x)$ の定義域が実数全体のときは、 $y=f(x)$ のグラフは次のようになる。
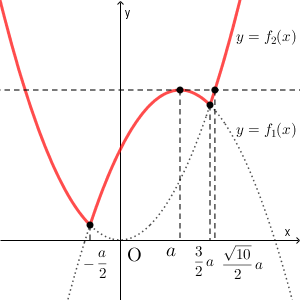
グラフより、 $-\dfrac{1}{2}a\leqq x \leqq \dfrac{3}{2}a$ のときに $f_1(x)\geqq f_2(x)$ なので、 $x$ が正のときに $f(x)\geqq f(-x)$ となることがわかる。以下では、区間の右端 $1$ と $a$, $\dfrac{\sqrt{10}}{2}a$ との大小関係によって場合分けをして考える。
(i) $a\gt 1$ のとき

区間の右端で最大となるので、最大値は\[ f_1(1)=-1^2+2a\cdot 1+\frac{3}{2}a^2= \frac{3}{2}a^2+2a-1 \]である。
(ii) $a\leqq 1 \lt \dfrac{\sqrt{10}}{2}a$ のとき、つまり、 $\dfrac{\sqrt{10}}{5}\lt a \leqq 1$ のとき
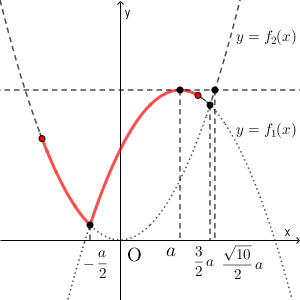
$x=a$ で最大となるので、最大値は\[ f_1(a)=\frac{5}{2}a^2 \]である。
(iii) $\dfrac{\sqrt{10}}{2}a\leqq 1$ のとき、つまり、 $0\lt a\leqq \dfrac{\sqrt{10}}{5}$ のとき
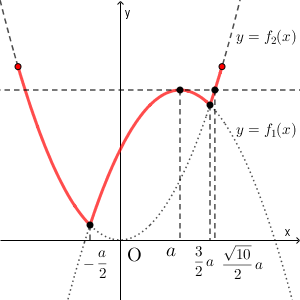
最大値は $x=\pm 1$ のときの値なので 、最大値は\[ f_2(1)=1 \]である。
以上から、最大値は
・ $0\lt a\leqq \dfrac{\sqrt{10}}{5}$ のとき: $1$
・ $\dfrac{\sqrt{10}}{5}\lt a\leqq 1$ のとき: $\dfrac{5}{2}a^2$
・ $a\gt 1$ のとき: $\dfrac{3}{2}a^2+2a-1$
となる。(答)





