京都大学 文系 2020年度 第1問 解説
問題編
問題
$a$ を負の実数とする。 $xy$ 平面上で曲線 $C:y=|x|x-3x+1$ と直線 $\ell:y=x+a$ のグラフが接するときの $a$ の値を求めよ。このとき、 $C$ と $\ell$ で囲まれた部分の面積を求めよ。
考え方
$a$ を求めるところまでは、二次関数の問題として考えることができます。面積は少し計算が面倒です。数学IIIの積分の計算を知っていたら少しルールの計算が楽になりますが、数学IIの範囲では面倒なまま計算することになります。
解答編
問題
$a$ を負の実数とする。 $xy$ 平面上で曲線 $C:y=|x|x-3x+1$ と直線 $\ell:y=x+a$ のグラフが接するときの $a$ の値を求めよ。このとき、 $C$ と $\ell$ で囲まれた部分の面積を求めよ。
解答
$y=x+a$ が $C$ の $x\geqq 0$ の部分で接するとすると、接点の $x$ 座標は
\begin{eqnarray}
x^2-3x+1 &=& x+a \\[5pt]
x^2-4x+(1-a) &=& 0 \\[5pt]
\end{eqnarray}の重解である。判別式は $0$ なので
\begin{eqnarray}
4^2-4(1-a) &=& 0 \\[5pt]
a &=& -3 \\[5pt]
\end{eqnarray}となり、このとき $x=2$ となることがわかる。
$x\lt 0$ の部分で接するとすると、接点の $x$ 座標は
\begin{eqnarray}
-x^2-3x+1 &=& x+a \\[5pt]
-x^2-4x+(1-a) &=& 0 \\[5pt]
\end{eqnarray}の重解である。判別式は $0$ なので
\begin{eqnarray}
4^2+4(1-a) &=& 0 \\[5pt]
a &=& 5 \\[5pt]
\end{eqnarray}となり、 $a\lt 0$ ではない。
以上から、 $a=-3$ で、接点の $x$ 座標は $2$ であることがわかる。グラフは以下のようになる。
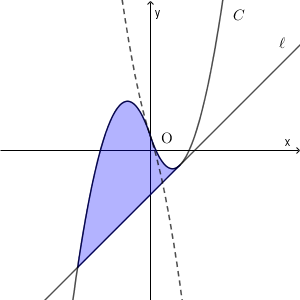
接点以外の共有点は、 $x\lt 0$ の範囲にある。その $x$ 座標は
\begin{eqnarray}
-x^2-3x+1 &=& x-3 \\[5pt]
x^2+4x-4 &=& 0 \\[5pt]
x &=& -2\pm 2\sqrt{2} \\[5pt]
\end{eqnarray}のうち、負の値なので、 $x=-2-2\sqrt{2}$ である。
以上から、 $C$ と $\ell$ で囲まれた部分の面積は
\begin{eqnarray}
& &
\int_{-2-2\sqrt{2} }^0 \left\{ (-x^2-3x+1) -(x-3) \right\} dx \\
& &
+\int_0^2 \left\{ (x^2-3x+1) -(x-3) \right\} dx \\[5pt]
&=&
\int_{-2-2\sqrt{2} }^0 ( -x^2-4x+4 ) dx \\
& &
+\int_0^2 (x^2-4x+4) dx \\[5pt]
&=&
\left[ -\dfrac{x^3}{3}-2x^2+4x \right]_{-2-2\sqrt{2} }^0 \\
& &
+\left[ \dfrac{x^3}{3}-2x^2+4x \right]_0^2 \\[5pt]
&=&
\dfrac{(-2-2\sqrt{2})^3}{3}+2(-2-2\sqrt{2})^2 \\
& &
-4(-2-2\sqrt{2}) +\left(\frac{8}{3}-2\cdot 2^2+4\cdot 2\right) \\[5pt]
&=&
-\dfrac{8(1+\sqrt{2})^3}{3}+8(1+\sqrt{2})^2 \\
& &
+8+8\sqrt{2} +\frac{8}{3} \\[5pt]
&=&
-\dfrac{8(1+3\sqrt{2}+6+2\sqrt{2}) }{3}+8(3+2\sqrt{2}) \\
& &
+\frac{32}{3}+8\sqrt{2} \\[5pt]
&=&
-\frac{56}{3}-\frac{40}{3}\sqrt{2}+24+16\sqrt{2} \\
& &
+\frac{32}{3}+8\sqrt{2} \\[5pt]
&=&
16+\frac{32}{3}\sqrt{2}
\end{eqnarray}と求められる。
(終)
別解
積分の計算は、数学IIIの内容を使えば、次のように求めることもできます。
\begin{eqnarray}
& &
\int_{-2-2\sqrt{2} }^0 \left\{ (-x^2-3x+1) -(x-3) \right\} dx \\
& &
+\int_0^2 \left\{ (x^2-3x+1) -(x-3) \right\} dx \\[5pt]
&=&
\int_0^{-2-2\sqrt{2} } ( x^2+4x-4 ) dx \\
& &
+\int_0^2 (x^2-4x+4) dx \\[5pt]
&=&
\int_0^{-2-2\sqrt{2} } \{(x+2)^2-8\} dx \\
& &
+\int_0^2 (x-2)^2 dx \\[5pt]
&=&
\left[ \dfrac{(x+2)^3}{3}-8x \right]_0^{-2-2\sqrt{2} } \\
& &
+\left[ \dfrac{(x-2)^3}{3} \right]_0^2 \\[5pt]
&=&
\dfrac{(-2-2\sqrt{2}+2)^3}{3}-8(-2-2\sqrt{2}) \\
& &
-\dfrac{(0+2)^3}{3} -\dfrac{(0-2)^3}{3} \\[5pt]
&=&
-\dfrac{16\sqrt{2} }{3}+16+16\sqrt{2}-\dfrac{8}{3}+\dfrac{8}{3} \\[5pt]
&=&
16+\frac{32}{3}\sqrt{2}
\end{eqnarray}





