京都大学 文系 2015年度 第4問 解説
問題編
【問題】
$xyz$空間の中で、$(0,0,1)$を中心とする半径1の球面$S$を考える。点Qが$(0,0,2)$以外のS上の点を動くとき、点Qと点$\mathrm{ P }(1,0,2)$の2点を通る直線lと平面$z=0$との交点をRとおく。Rの動く範囲を求め、図示せよ。
【考え方】
この問題は、出発の仕方が難しいです。点Qに対して点Rがどう決まるかを考え、そのあとで点Qを動かす、というような感じで解きたくなりますが、その方法ではなかなか解けません。点Qの動く範囲が球面なので、最後の「点Qを動かす」の部分で計算が行き詰ってしまいます。
なので、発想を変え、点Rに着目して次のように考えます。2点PとRを通る直線が球面と共有点を持つように点Rを動かす、と。この発想ができないとこの問題を解くのは難しいです。
解答編
【問題】
$xyz$空間の中で、$(0,0,1)$を中心とする半径1の球面$S$を考える。点Qが$(0,0,2)$以外のS上の点を動くとき、点Qと点$\mathrm{ P }(1,0,2)$の2点を通る直線lと平面$z=0$との交点をRとおく。Rの動く範囲を求め、図示せよ。
【解答】
点Rの座標を $(X,Y,0)$とする。このとき、直線PR上の点は、実数tを用いて
\begin{eqnarray}
& & (1,0,2)+t\{ (X,Y,0) - (1,0,2) \} \\
&=& ( 1 + t(X-1) , tY, 2-2t )
\end{eqnarray}と書ける。
点Qが$(0,0,2)$以外のS上の点を動くとき、直線PQは必ず平面$z=0$と交わる。このとき、その交点Rの座標とある実数$t$を用いて、Qの座標は上のように書ける。よって、点$( 1 + t(X-1) , tY, 2-2t )$が球面$S:x^2+y^2+(z-1)^2=1$上にあるような実数$t$の存在する領域が、求めるものである。
つまり、次が実数解を持つ領域が求めるものである。
\begin{eqnarray}
\{ 1+t(X-1) \}^2 + (tY)^2 + (2-2t-1)^2 &=& 1 \\
\{ t(X-1)+1 \}^2 + Y^2t^2 + 4t^2-4t+1 &=& 1 \\
(X^2-2X+1+Y^2+4)t^2 +(2X-2-4)t+1+1&=&1 \\
(X^2-2X+Y^2+5)t^2 +(2X-6)t+1&=&0
\end{eqnarray}
この判別式が0以上なので、
\begin{eqnarray}
(2X-6)^2-4 (X^2-2X+Y^2+5) &\geqq& 0 \\
X^2-6X+9 - X^2+2X-Y^2-5 &\geqq& 0 \\
-4X+4 -Y^2 &\geqq& 0 \\
X &\leqq& -\frac{1}{4}Y^2+1 \\
\end{eqnarray}となる。
よって、これが求める範囲であり、図示すると次のようになる(境界線の点を含む)。
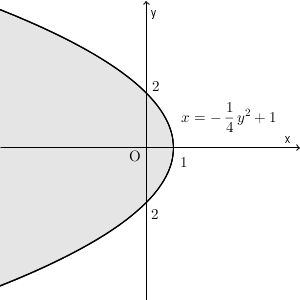
【解答終】
【解説】
Qを動かすという発想から抜けれるかがポイントです。しかも、3次元の問題なので、文系にはなかなか厳しい問題だと思います。
ちなみに、この問題の答えは、「点$\mathrm{ P }(1,0,2)$に太陽(光源)があった場合、平面$z=0$にできる球面$S$の影」と考えることができます。つまり、影は放物線になる、ということなんですね。きれいな答えです。なお、光源がより高いところにある(この問題では、$z\gt 2$)場合は、影は楕円になり、より低い所にある場合は、影は双曲線になります。





