京都大学 文系 2015年度 第3問 解説
問題編
【問題】
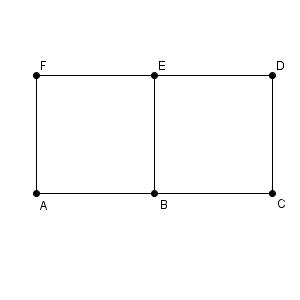
6個の点 A, B, C, D, E, F が下図のように長さ1の線分で結ばれているとする。各線分をそれぞれ独立に確率$\displaystyle \frac{1}{2}$で赤または黒で塗る。赤く塗られた線分だけを通って点Aから点Eに至る経路がある場合はそのうちで最短のものの長さを$X$とする。そのような経路がない場合は$X$を0とする。このとき、$n=0,2,4$について、$X=n$となる確率を求めよ。
【考え方】
少し複雑なので、場合分けしながら確率を計算しなければいけません。何で場合分けをするか、いくつかパターンはありえますが、AからEにいける経路は3パターンしかないので、経路に注目して場合分けするのがよさそうです。
解答編
【問題】
6個の点 A, B, C, D, E, F が下図のように長さ1の線分で結ばれているとする。各線分をそれぞれ独立に確率$\displaystyle \frac{1}{2}$で赤または黒で塗る。赤く塗られた線分だけを通って点Aから点Eに至る経路がある場合はそのうちで最短のものの長さを$X$とする。そのような経路がない場合は$X$を0とする。このとき、$n=0,2,4$について、$X=n$となる確率を求めよ。
【解答】
AからEへの最短経路は、下の3パターンしかない。
(1) A→F→E
(2) A→B→E
(3) A→B→C→D→E
$X=2$となる確率は、(1)または(2)の経路がとれる確率である。(1)の経路がとれる確率は、$\frac{1}{4}$、(2)の経路がとれる確率も、$\frac{1}{4}$である。また、(1)と(2)両方の経路がとれる確率は、$\frac{1}{16}$である。以上から、$X=2$となる確率は、
\begin{eqnarray}
\frac{1}{4}+\frac{1}{4}-\frac{1}{16}=\frac{7}{16}
\end{eqnarray}となる。
$X=4$となる確率は、(1)と(2)の経路がとれず、(3)の経路がとれる確率である。(1)の経路がとれない確率は、AFかFEが通れない確率なので、$\frac{3}{4}$となる。(2)の経路がとれなくて(3)の経路がとれるためには、ABが通れる、EBが通れない、BC・CD・EFが通れる確率である。よって、$X=4$となる確率は、
\begin{eqnarray}
& &
\frac{3}{4} \cdot \frac{1}{2} \cdot \frac{1}{2} \cdot \frac{1}{2} \cdot \frac{1}{2} \cdot \frac{1}{2} \\[5pt]
&=&\frac{3}{128}
\end{eqnarray}となる。

$X=0$となる確率は、(1)(2)(3)のどの経路もとれない確率である。(1)の経路がとれない確率は、AFかFEが通れない確率なので、$\frac{3}{4}$となる。(2)と(3)の経路がとれないときは、ABが通れないときか、「ABが通れてEBが通れず、BC・CD・DEのどれかが通れないとき」となる。よって、$X=0$となる確率は、
\begin{eqnarray}
& &
\frac{3}{4}\left\{ \frac{1}{2} + \frac{1}{2} \cdot \frac{1}{2} \left( 1-\frac{1}{2^3} \right) \right\} \\[5pt]
&=& \frac{3}{4} \cdot \frac{23}{32} = \frac{69}{128}
\end{eqnarray}となる。
よって、$X=0,2,4$となる確率は、それぞれ $\displaystyle \frac{69}{128}, \frac{7}{16}, \frac{3}{128}$ となる。
【解答終】
【解説】
まず、AFEとABEの両方の経路が通れる場合があることに注意しないといけません。また、ABEとABCDEは、ABがかぶっていることにも注意が必要です。どちらも、落ち着いて考えればつまづくことはないと思います。
$X$は0, 2, 4の値しかとりえないので、0となる確率は、2, 4となる確率を1から引いて求めてもOKです。上の解答では、計算間違いがないことを確認できるように、0の場合も個別に算出しています。





