京都大学 文系 2015年度 第1問 解説
問題編
【問題】
直線$y=px+q$が、$y=x^2-x$のグラフとは交わるが、$y=|x|+|x-1|+1$のグラフとは交わらないような$(p,q)$の範囲を図示し、その面積を求めよ。
【考え方】
「交わる」は、判別式が0以上となる範囲を考えればいいですね。「交わらない」の方は少しめんどうです。グラフを描いてみて、交わらない条件を考えていきます。
範囲が求まれば、面積を求めるのは大変ではありません。
解答編
【問題】
直線$y=px+q$が、$y=x^2-x$のグラフとは交わるが、$y=|x|+|x-1|+1$のグラフとは交わらないような$(p,q)$の範囲を図示し、その面積を求めよ。
【解答】
$y=px+q$と$y=x^2-x$とのグラフが交わるとき、$x^2-x=px+q$は実数解をもつ。つまり、判別式が0以上なので、
\begin{eqnarray}
(-1-p)^2-4(-q) &\geqq& 0 \\
q &\geqq& - \frac{1}{4} (p+1)^2 \ \ \cdots (1)
\end{eqnarray}となる。
$y=|x|+|x-1|+1$は、$x$の値によって次のように変形できる。
\begin{eqnarray}
y =
\left\{
\begin{array}{1}
2x \ & &(x\geqq 1) \\
2 \ & &(1 \gt x\gt 0) \\
-2x+2 \ & &( 0 \geqq x)
\end{array}
\right.
\end{eqnarray}
よって、グラフは次のようになる。
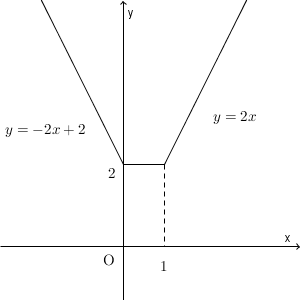
$f(x)=px+q$、$g(x)=|x|+|x-1|+1$ とする。
$p\gt 2$とすると、$x\geqq1$で$y=2x$と交わらないためには、$f(1)\gt 2$である必要があるが、このとき$y=f(x)$と$y=g(x)$は$x\lt1$で交わってしまう。
また、$p\lt -2$とすると、$x\leqq 0$で$y=-2x+2$と交わらないためには、$f(0)\gt 2$である必要があるが、このとき$y=f(x)$と$y=g(x)$は$x\gt 0$で交わってしまう。
よって、2つのグラフが交わらないためには、$-2\leqq p \leqq 2$が必要である。
$0\leqq p \leqq 2$のとき、2つのグラフが交わらないためには、$g(1)\lt 2$が必要であり、これを満たせば交わることはない。このときの条件は、「$0\leqq p \leqq 2$ かつ $q\lt -p+2$」と書ける。この条件を(2)と書く。
$-2\leqq p \lt 0$のとき、2つのグラフが交わらないためには、$g(0)\lt 2$が必要であり、これを満たせば交わることはない。このときの条件は、「$-2\leqq p \lt 0$ かつ $q\lt 2$」と書ける。この条件を(3)と書く。
以上から、$(p,q)$の範囲は、(1)(2)(3)すべてに含まれる領域なので、以下の通りとなる。
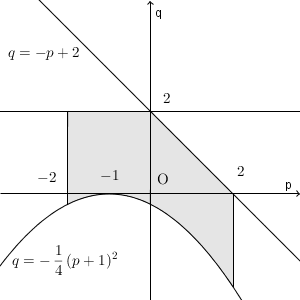
ただし、境界は$q=-p+2,q=2$上の点以外をすべて含む。
また、この領域の面積は、
\begin{eqnarray}
& &
\int _{-2}^2 \left\{ 2+\frac{1}{4}(p+1)^2 \right\}dp - \frac{1}{2}\cdot 2\cdot 2 \\[5pt]
&=&
\left[ 2p + \frac{1}{4}\cdot \frac{1}{3}(p+1)^3 \right]_{-2}^2 - 2 \\[5pt]
&=&
\left( 4 + \frac{1}{12}\cdot 27 + 4 +\frac{1}{12}\cdot 1 \right) - 2 \\[5pt]
&=&
\frac{25}{3}
\end{eqnarray}
となる。
【解答終】
【解説】
「交わらない」の条件を漏れなく考えるのが少し大変です。傾きが2より大きい場合、-2より小さい場合、その間の場合など、さまざまな場合で交わらない条件を考えないといけないので、漏れなく条件を書き出すのは少し難しいです。





