京都大学 文系 2013年度 第1問 解説
問題編
問題
$a$ を $2$ 以上の実数とし、 $f(x)=(x+a)(x+2)$ とする。このとき $f(f(x))\gt 0$ がすべての実数 $x$ に対して成り立つような $a$ の範囲を求めよ。
考え方
$f(x)$ の中に $f(x)$ が入っていて、このままだとよくわからないですが、まずは、 $f(x)$ がどうなっていればいいのかを考えましょう。
解答編
問題
$a$ を $2$ 以上の実数とし、 $f(x)=(x+a)(x+2)$ とする。このとき $f(f(x))\gt 0$ がすべての実数 $x$ に対して成り立つような $a$ の範囲を求めよ。
解答
$f(x)\gt 0$ は「 $x\lt -a$ または $x\gt -2$ 」と同値である。よって、 $f(f(x))\gt 0$ は、「 $f(x)\lt -a$ または $f(x)\gt -2$ 」と同値である。
\begin{eqnarray} f(x) &=& (x+a)(x+2) \\[5pt] &=& x^2+(a+2)x+2a \\[5pt] &=& \left(x+\frac{a+2}{2}\right)^2 +2a-\frac{(a+2)^2}{4} \\[5pt] &=& \left(x+\frac{a+2}{2}\right)^2 +\frac{8a-a^2-4a-4}{4} \\[5pt] &=& \left(x+\frac{a+2}{2}\right)^2 +\dfrac{-a^2+4a-4}{4} \\[5pt] \end{eqnarray}なので、 $f(x)$ は $\dfrac{-a^2+4a-4}{4}$ 以上の実数値をすべてとる。なので、「 $f(x)\lt -a$ または $f(x)\gt -2$ 」がすべての実数 $x$ について成り立つことは、 $\dfrac{-a^2+4a-4}{4}\gt -2$ が成り立つことと同値である。 \begin{eqnarray} \dfrac{-a^2+4a-4}{4} \gt -2 \\[5pt] a^2-4a+4 \lt 8 \\[5pt] a^2-4a-4 \lt 0 \\[5pt] \end{eqnarray}であり、 $a^2-4a-4=0$ の解は $a=2\pm\sqrt{2^2+4}=-2\pm2\sqrt{2}$ だから、 $\dfrac{-a^2+4a-4}{4}\gt -2$ が成り立つことは\[ 2-2\sqrt{2}\lt a\lt 2+2\sqrt{2} \]が成り立つことと同値である。$a\geqq 2$ なので、求める $a$ の範囲は $2\leqq a\lt 2+2\sqrt{2}$ となる。
(解答終)
解説
$x$, $f(x)$, $f(f(x))$ と動くものが3つありますが、すべて $f(x)$ にそろえると考えやすくなります。 $f(f(x))\gt 0$ となることは、 「 $f(x)\lt -a$ または $f(x)\gt -2$ 」と同値であり、 $f(x)$ は $\dfrac{-a^2+4a-4}{4}$ 以上の値をすべてとります。
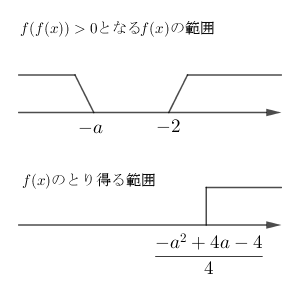
このことから、 $\dfrac{-a^2+4a-4}{4}$ 以上の範囲が、「 $f(x)\lt -a$ または $f(x)\gt -2$ 」の範囲にすっぽり入ってしまえば、つねに $f(f(x))\gt 0$ となり、それ以外の場合は該当しないので、上のような解答となります。





