センター試験 数学II・数学B 2016年度 第4問 解説
問題編
問題
四面体OABC において、$\lvert\overrightarrow{ \mathrm{OA} }\rvert=3$、$|\overrightarrow{ \mathrm{OB} }|=|\overrightarrow{ \mathrm{OC} }|=2$、$\angle \mathrm{AOB}=\angle \mathrm{BOC}=\angle \mathrm{COA}=60^{\circ}$ であるとする。また、辺OA上に点P をとり、辺BC上に点Q をとる。以下、$\overrightarrow{ \mathrm{OA} }=\vec{ a }$、$\overrightarrow{ \mathrm{OB} }=\vec{ b }$、$\overrightarrow{ \mathrm{OC} }=\vec{ c }$ とおく。
(1) $0 \leqq s \leqq 1$、$0 \leqq t \leqq 1$ であるような実数s、t を用いて、$\overrightarrow{ \mathrm{OP} }=s\vec{a}$、$\overrightarrow{ \mathrm{OQ} }=(1-t)\vec{b}+t\vec{c}$ と表す。$\vec{a}\cdot\vec{b} = \vec{a}\cdot\vec{c}=\myBox{ア}$、$\vec{b}\cdot\vec{c}=\myBox{イ}$であることから\[ |\overrightarrow{\mathrm{PQ} }|^2 =
\Big(\myBox{ウ}s-\myBox{エ}\Big)^2+\Big(\myBox{オ}t-\myBox{カ}\Big)^2+\myBox{キ} \]となる。したがって、$|\overrightarrow{\mathrm{PQ} }|$ が最小となるのは、$s=\dfrac{\myBox{ク}}{\myBox{ケ}}$、$t=\dfrac{\myBox{コ}}{\myBox{サ}}$のときであり、このとき $|\overrightarrow{\mathrm{PQ} }|=\sqrt{\myBox{シ}}$ となる。(2) 三角形ABC の重心を G とする。$|\overrightarrow{ \mathrm{PQ} }|=\sqrt{\mybox{シ}}$のとき、三角形GPQ の面積を求めよう。
$\overrightarrow{ \mathrm{OA} } \cdot \overrightarrow{ \mathrm{PQ} } = \myBox{ス}$ から、$\angle\mathrm{APQ}=\myBox{セソ}^{\circ}$ である。したがって、三角形APQ の面積は$\sqrt{\myBox{タ}}$である。また\[ \overrightarrow{ \mathrm{OG} } = \frac{\myBox{チ}}{\myBox{ツ}}\overrightarrow{ \mathrm{OA} } + \frac{\myBox{テ}}{\myBox{ト}}\overrightarrow{ \mathrm{OQ} } \]であり、点G は線分AQ を $\myBox{ナ}:1$ に内分する点である。
以上のことから、三角形GPQ の面積は $\dfrac{\sqrt{\myBox{ニ}}}{\myBox{ヌ}}$ である。
考え方
空間におけるベクトルです。3次元だと図をかくのが大変ですが、(1)は特に図をかかなくても解けます。計算はごちゃごちゃしやすいですが、難しくはありません。誘導に従って解けば、最後まで行けるでしょう。
(2)はさすがに図をかかないと厳しいです。ベクトルの式から、P や Q がどういう点であるかを把握することが重要です。最後の三角形の面積を求めるところは、辺の長さの比で出すことができます。
空間ベクトルにしては解きやすい問題です。
解答編
問題
四面体OABC において、$\lvert\overrightarrow{ \mathrm{OA} }\rvert=3$、$|\overrightarrow{ \mathrm{OB} }|=|\overrightarrow{ \mathrm{OC} }|=2$、$\angle \mathrm{AOB}=\angle \mathrm{BOC}=\angle \mathrm{COA}=60^{\circ}$ であるとする。また、辺OA上に点P をとり、辺BC上に点Q をとる。以下、$\overrightarrow{ \mathrm{OA} }=\vec{ a }$、$\overrightarrow{ \mathrm{OB} }=\vec{ b }$、$\overrightarrow{ \mathrm{OC} }=\vec{ c }$ とおく。
(1) $0 \leqq s \leqq 1$、$0 \leqq t \leqq 1$ であるような実数s、t を用いて、$\overrightarrow{ \mathrm{OP} }=s\vec{a}$、$\overrightarrow{ \mathrm{OQ} }=(1-t)\vec{b}+t\vec{c}$ と表す。$\vec{a}\cdot\vec{b} = \vec{a}\cdot\vec{c}=\myBox{ア}$、$\vec{b}\cdot\vec{c}=\myBox{イ}$であることから\[ |\overrightarrow{\mathrm{PQ} }|^2 =
\Big(\myBox{ウ}s-\myBox{エ}\Big)^2+\Big(\myBox{オ}t-\myBox{カ}\Big)^2+\myBox{キ} \]となる。したがって、$|\overrightarrow{\mathrm{PQ} }|$ が最小となるのは、$s=\dfrac{\myBox{ク}}{\myBox{ケ}}$、$t=\dfrac{\myBox{コ}}{\myBox{サ}}$のときであり、このとき $|\overrightarrow{\mathrm{PQ} }|=\sqrt{\myBox{シ}}$ となる。
解説
よって、
\begin{eqnarray}
|\overrightarrow{ \mathrm{PQ} }|^2
&=&
|-s\vec{a}+(1-t)\vec{b}+t\vec{c}|^2 \\[5pt]
&=&
s^2|\vec{a}|^2
+(1-t)^2|\vec{b}|^2
+t^2|\vec{c}|^2
\\
& &
-2s(1-t)\vec{ a } \cdot \vec{ b }
+2t(1-t)\vec{ b } \cdot \vec{ c }
-2st\vec{ c } \cdot \vec{ a } \\[5pt]
&=&
9s^2
+4(1-t)^2
+4t^2
\\
& &
-6s(1-t)
+4t(1-t)
-6st
\\[5pt]
&=&
9s^2
+4t^2-8t+4
+4t^2
\\
& &
-6s+6st
+4t -4t^2
-6st
\\[5pt]
&=&
9s^2-6s
+4t^2-4t
+4 \\
&=&
(3s-1)^2
+(2t-1)^2
+2 \\
\end{eqnarray}と計算できます。
この式から、$|\overrightarrow{ \mathrm{PQ} }|$ が最小となるのは、$s=\dfrac{1}{3}$、$t=\dfrac{1}{2}$ のときで、その時の値は、$\sqrt{2}$ となることがわかります。
解答
ア:3
イ:2
ウエオカキ:31212
クケコサシ:13122
解答編 つづき
問題
(2) 三角形ABC の重心を G とする。$|\overrightarrow{ \mathrm{PQ} }|=\sqrt{\mybox{シ}}$のとき、三角形GPQ の面積を求めよう。
$\overrightarrow{ \mathrm{OA} } \cdot \overrightarrow{ \mathrm{PQ} } = \myBox{ス}$ から、$\angle\mathrm{APQ}=\myBox{セソ}^{\circ}$ である。したがって、三角形APQ の面積は$\sqrt{\myBox{タ}}$である。
解説
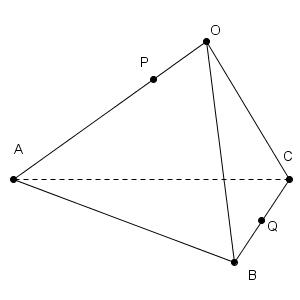
図の概形は次のようになります。

$\overrightarrow{ \mathrm{PQ} }=-s\vec{a}+(1-t)\vec{b}+t\vec{c}$ であり、(1)の最後で求めた通り、$s=\dfrac{1}{3}$、$t=\dfrac{1}{2}$ です。よって、
\begin{eqnarray}
\overrightarrow{ \mathrm{OA} } \cdot \overrightarrow{ \mathrm{PQ} }
&=&
\vec{a} \cdot \left( -\frac{1}{3}\vec{a}+\frac{1}{2}\vec{b}+\frac{1}{2}\vec{c} \right) \\
&=&
-\frac{1}{3} \cdot 9 + \frac{1}{2} \cdot 3 + \frac{1}{2} \cdot 3 = 0 \\
\end{eqnarray}となります。
このことから、OAとPQは垂直であることがわかるので、$\angle \mathrm{APQ}=90^{\circ}$となります。
$\mathrm{OA}=3$ より、$\mathrm{OP}=\dfrac{1}{3}\mathrm{OA}=1$ だから、$\mathrm{AP}=2$ です。また、(1)の結果より、PQ の長さは $\sqrt{2}$ です。よって、直角三角形APQ の面積は、\[ \frac{1}{2}\times 2 \times \sqrt{2}=\sqrt{2} \]となります。
解答
ス:0
セソ:90
タ:2
解答編
問題
また\[ \overrightarrow{ \mathrm{OG} } = \frac{\myBox{チ}}{\myBox{ツ}}\overrightarrow{ \mathrm{OA} } + \frac{\myBox{テ}}{\myBox{ト}}\overrightarrow{ \mathrm{OQ} } \]であり、点G は線分AQ を $\myBox{ナ}:1$ に内分する点である。
以上のことから、三角形GPQ の面積は $\dfrac{\sqrt{\myBox{ニ}}}{\myBox{ヌ}}$ である。
解説
$t=\dfrac{1}{2}$ なので、Q はBC の中点です。また、G は三角形ABC の重心だから、
$\overrightarrow{ \mathrm{OG} } = \dfrac{1}{3}\overrightarrow{ \mathrm{OA} } + \dfrac{2}{3}\overrightarrow{ \mathrm{OQ} }$ であり、G は AQ を 2:1 に内分する点です。

以上のことから、三角形GPQ の面積は、三角形APQ の $\dfrac{1}{3}$ 倍となるので、$\dfrac{\sqrt{2}}{3}$ となります。
解答
チツテトナ:13232
ニヌ:23





