センター試験 数学II・数学B 2016年度 第2問 解説

問題編

【問題】
座標平面上で、放物線$\displaystyle y=\frac{1}{2}x^2+\frac{1}{2}$を$C_1$とし、放物線$\displaystyle y=\frac{1}{4} x^2$を$C_2$とする。

(1)
実数aに対して、2直線$x=a$、$x=a+1$と$C_1$、$C_2$で囲まれた図形Dの面積Sは
\begin{eqnarray} S &=& \int_a^{a+1} \left(\frac{1}{[ア]}x^2 + \frac{1}{[イ]} \right)dx \\[5pt] &=& \frac{a^2}{[ウ]}+\frac{a}{[エ]}+\frac{[オ]}{[カキ]} \end{eqnarray} である。Sは$\displaystyle a=\frac{[クケ]}{[コ]}$で最小値$\displaystyle \frac{[サシ]}{[スセ]}$をとる。

(2)
4点$(a,0),(a+1,0),(a+1,1),(a,1)$を頂点とする正方形をRで表す。aが$a\geqq 0$の範囲を動くとき、正方形Rと(1)の図形Dの共通部分の面積をTとおく。Tが最大となるaの値を求めよう。

直線$y=1$は、$C_1$と$(\pm[ソ],1)$で、$C_2$と$(\pm[タ],1)$で交わる。したがって、正方形Rと図形Dの共通部分が空集合にならないのは、$0\leqq a \leqq [チ]$のときである。

$[ソ] \leqq a \leqq [チ]$のとき、正方形Rは放物線$C_1$とx軸の間にあり、この範囲でaが増加するとき、Tは[ツ]。[ツ]に当てはまるものを、次の0～2のうちから一つ選べ。

0: 増加する、　1:減少する、　2:変化しない

したがって、Tが最大になるaの値は、$0\leqq a \leqq [ソ]$の範囲にある。

$0\leqq a \leqq [ソ]$のとき、(1)の図形Dのうち、正方形Rの外側にある部分の面積Uは
\[
U=\frac{a^3}{[テ]}+\frac{a^2}{[ト]}
\]
である。よって、$0 \leqq a \leqq[ソ]$において
\[
T=-\frac{a^3}{[ナ]}-\frac{a^2}{[ニ]}+\frac{a}{[ヌ]}+\frac{[オ]}{[カキ]} \quad \cdots ①
\]
である。①の右辺の増減を調べることにより、Tは
\[
a=\frac{[ネノ]+\sqrt{[ハ]} }{[ヒ]}
\]
で最大値をとることがわかる。

【考え方】
(1)はグラフを描けば、何を計算するかはそんなに難しくないでしょう。微分・積分の範囲としては、基本的な問題です。

(2)は誘導は丁寧ですが、意図を読み取るにはきちんとグラフが描けないといけません。$a=1$の前後で状況がどう変わるかを把握する必要があります。

Uが出てくるあたりから計算量が増えていきますが、センター試験ではよくある分量です。最後は、最大値まで求める必要はないので、無駄な計算はしないようにしましょう。

---

解答編

【問題】
座標平面上で、放物線$\displaystyle y=\frac{1}{2}x^2+\frac{1}{2}$を$C_1$とし、放物線$\displaystyle y=\frac{1}{4} x^2$を$C_2$とする。

(1)
実数aに対して、2直線$x=a$、$x=a+1$と$C_1$、$C_2$で囲まれた図形 class="i">Dの面積Sは
\begin{eqnarray} S &=& \int_a^{a+1} \left(\frac{1}{[ア]}x^2 + \frac{1}{[イ]} \right)dx \\[5pt] &=& \frac{a^2}{[ウ]}+\frac{a}{[エ]}+\frac{[オ]}{[カキ]} \end{eqnarray} である。Sは$\displaystyle a=\frac{[クケ]}{[コ]}$で最小値$\displaystyle \frac{[サシ]}{[スセ]}$をとる。

【解説】
図を書くと、こういう状況ですね。

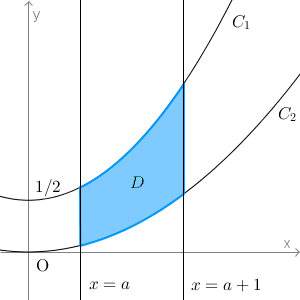
$C_1$ は $C_2$ より上にあるので、
\begin{eqnarray} S&=&\int^{a+1}_a \left(\frac{1}{2}x^2+\frac{1}{2} - \frac{1}{4}x^2 \right) dx \\ &=&\int^{a+1}_a \left(\frac{1}{4}x^2+\frac{1}{2} \right) dx \end{eqnarray}となります。

これを計算すると
\begin{eqnarray} S&=& \left[ \frac{x^3}{12} + \frac{x}{2} \right]^{a+1}_a \\[5pt] &=& \frac{(a+1)^3-a^3}{12} + \frac{a+1-a}{2} \\[5pt] &=& \frac{3a^2+3a+1}{12} + \frac{6}{12} \\[5pt] &=& \frac{a^2}{4}+\frac{a}{4}+\frac{7}{12} \\ \end{eqnarray}となります。

このSが最小となるときを考えます。次のように式変形をします。
\begin{eqnarray} S&=& \frac{a^2}{4}+\frac{a}{4}+\frac{7}{12} \\ &=& \frac{1}{4} \left( a + \frac{1}{2} \right)^2 -\frac{1}{16} +\frac{7}{12} \\ &=& \frac{1}{4} \left( a + \frac{1}{2} \right)^2 +\frac{25}{48} \\ \end{eqnarray} このことから、Sは、$\displaystyle a=-\frac{1}{2}$のときに、最小値$\displaystyle \frac{25}{48}$をとることがわかります。

【解答】
アイ：42
ウエオカキ：44712
クケコ：-12
サシスセ：2548

【問題】
(2)
4点$(a,0),(a+1,0),(a+1,1),(a,1)$を頂点とする正方形をRで表す。aが$a\geqq 0$の範囲を動くとき、正方形Rと(1)の図形Dの共通部分の面積をTとおく。Tが最大となるaの値を求めよう。

直線$y=1$は、$C_1$と$(\pm[ソ],1)$で、$C_2$と$(\pm[タ],1)$で交わる。したがって、正方形Rと図形Dの共通部分が空集合にならないのは、$0\leqq a \leqq [チ]$のときである。

【解説】
次のような状況です。

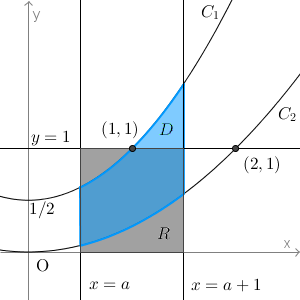
直線 $y=1$ と $C_1$ との交点は、 $1=\frac{1}{2}x^2+\frac{1}{2}$ を解けばよく、 $x=\pm 1$ であることがわかります。

また、 $C_2$ との交点は、 $1=\frac{1}{4}x^2$ を解けばよく、 $x=\pm 2$ であることがわかります。

このことから、正方形R（上のグレーの部分）と、(1)の図形D（上の青色の部分）が交わるのは、 $0 \leqq a\leqq 2$ のときであることがわかります。2より大きいと、図形Dは$y=1$よりも上にあるので、交わりません。

【解答】
ソ：1
タ：2
チ：2

【問題】
$[ソ] \leqq a \leqq [チ]$のとき、正方形Rは放物線$C_1$とx軸の間にあり、この範囲でaが増加するとき、Tは[ツ]。[ツ]に当てはまるものを、次の0～2のうちから一つ選べ。

0: 増加する、　1:減少する、　2:変化しない

【解説】
$1 \leqq a \leqq 2$ のとき、グラフは次のような状況になっています。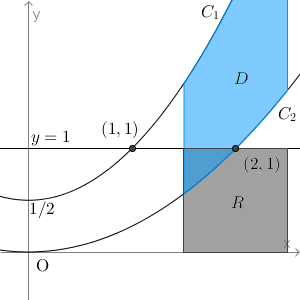

aが大きくなるほど、領域は右に移動していき、共通部分は小さくなっていきます。よって、Tは減少していきます。

【解答】
ツ：1

【問題】
したがって、Tが最大になるaの値は、$0\leqq a \leqq [ソ]$の範囲にある。

$0\leqq a \leqq [ソ]$のとき、(1)の図形Dのうち、正方形Rの外側にある部分の面積Uは
\[
U=\frac{a^3}{[テ]}+\frac{a^2}{[ト]}
\]
である。

【解説】
今までのことから、RとDが交わるのは、$0 \leqq a \leqq 2$のときで、$1\leqq a \leqq 2$のときはaが大きくなるほど面積Tが小さくなることがわかりました。これらから、Tが最大になるのは、$0 \leqq a \leqq 1$のときであることがわかります。

このとき、グラフは次のようになっています。

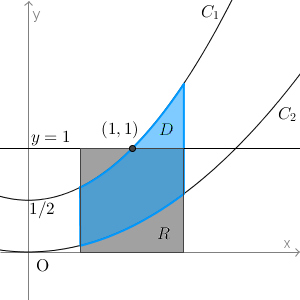
問題文にある「(1)の図形Dのうち、正方形Rの外側にある部分」というのは、 $y=1$ より上の部分ということですね。ここは、 $C_1$ と直線 $y=1$ 、直線 $x=a+1$ で囲まれた部分なので、この面積Uは、
\begin{eqnarray} U &=&\int^{a+1}_1 \left( \frac{1}{2}x^2 + \frac{1}{2} -1 \right) dx \\[5pt] &=& \left[ \frac{x^3}{6} -\frac{x}{2} \right]^{a+1}_1 \\[5pt] &=& \frac{a^3+3a^2+3a+1}{6} -\frac{a+1}{2} -\frac{1}{6} + \frac{1}{2} \\[5pt] &=& \frac{a^3}{6} + \frac{a^2}{2} \end{eqnarray}と求めることができます。

【解答】
テト：62

【問題】
よって、$0 \leqq a \leqq[ソ]$において
\[
T=-\frac{a^3}{[ナ]}-\frac{a^2}{[ニ]}+\frac{a}{[ヌ]}+\frac{[オ]}{[カキ]} \quad \cdots ①
\]
である。

【解説】

(1)で求めたSからUを引けばTになるので、
\begin{eqnarray} T &=& S-U \\ &=& \left( \frac{a^2}{4}+\frac{a}{4}+\frac{7}{12} \right) -\left( \frac{a^3}{6} + \frac{a^2}{2} \right) \\ &=& -\frac{a^3}{6}-\frac{a^2}{4}+\frac{a}{4}+\frac{7}{12} \end{eqnarray}となります。

なお、この式で、「オカキ」が出てきますが、このことが(1)のSを使うこと、つまり、$T=S-U$を使うことのヒントになっています。

【解答】
ナニヌ：644

【問題】
①の右辺の増減を調べることにより、Tは
\[
a=\frac{[ネノ]+\sqrt{[ハ]} }{[ヒ]}
\]
で最大値をとることがわかる。

【解説】
ここまでくれば、微分して増減表を書くだけですね。

先ほど求めた式
\[
T=-\frac{a^3}{6}-\frac{a^2}{4}+\frac{a}{4}+\frac{7}{12}
\]
をaで微分したものが0になるのは、
\begin{eqnarray} -\frac{a^2}{2}-\frac{a}{2}+\frac{1}{4}&=&0 \\[5pt] 2a^2 + 2a -1&=&0 \\ a&=&\frac{-2\pm\sqrt{2^2+8} }{4} \\ &=&\frac{-1\pm\sqrt{3} }{2} \\ \end{eqnarray}のときです。

増減表を書くと
\begin{array}{c|ccccc} a & 0 & \cdots & \frac{-1+\sqrt{3} }{2} & \cdots & 1 \\ \hline dT/da & & + & 0 & - & \\ \hline T & & \nearrow & & \searrow & \end{array} なので、$a=\frac{-1+\sqrt{3} }{2}$のときにTが最大になることがわかります。

【解答】
ネノハヒ：-132