東京大学理系 2016年度第4問解説

🕒 2016/02/26 🔄 2023/05/01

問題編

【問題】
zを複素数とする。複素数平面上の3点A$(1)$、B$(z)$、C$(z^2)$が鋭角三角形をなすようなzの範囲を求め、図示せよ。

【考え方】
どうやって計算するかで、計算量がかなり変わってくる問題です。平行移動や回転をしても三角形の形は変わらないので、計算しやすい形に変形してから考えます。ここでは、Aが原点に来るように平行移動し、Bが実軸上にくるように回転させてから考えると、ほとんど計算することなく解けます。

解答編

【問題】
zを複素数とする。複素数平面上の3点A$(1)$、B$(z)$、C$(z^2)$が鋭角三角形をなすようなzの範囲を求め、図示せよ。

【解答】
ABCが三角形となるとき、どの2点も重なってはいけないので、$z\ne 1$である。また、3点が一直線上に並んでもいけないので、zは実数ではない。逆にzが実数でないときは、ABCは三角形となる。

以下では、zは実数ではないと仮定する。

3点を実軸の負の方向に1だけ移動すると、3点はそれぞれ$(0)$、$(z-1)$、$(z^2-1)$に移動する。また、点$(z-1)$が実軸上の正の部分の$(1)$に来るように原点を中心に回転すると、3点はそれぞれ$(0)$、$(1)$、$(z+1)$に移動する。移動後も三角形の形は変わらないので、移動後の3点が鋭角三角形になる条件を考えればよい。

移動後の3点をそれぞれP、Q、Rとする。

$\angle \mathrm{ PQR }$が鋭角であることと、点R$(z+1)$の実部が1（Qの実部）より小さいことは同値。

$\angle \mathrm{ QRP }$が鋭角であることと、点R$(z+1)$が、点$(\frac{1}{2})$を中心とする半径$\frac{1}{2}$の円の外にいることは同値。

$\angle \mathrm{ RPQ }$が鋭角であることと、点R$(z+1)$の実部が0（Pの実部）より大きいことは同値。

以上から、zの範囲は、以下の色付けした部分となる。ただし、境界線は含まない。

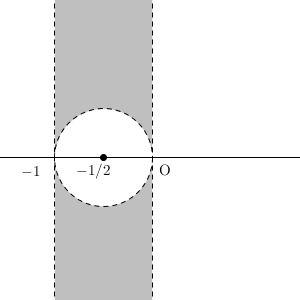
【解答終】