【標準】三角比と中線
ここでは、三角比を用いて中線の長さを求める問題を考えてみます。角の二等分線を用いた問題よりは出題頻度は低いですが、三角比の使い方を勉強するのにはいい材料なので紹介します。
例題
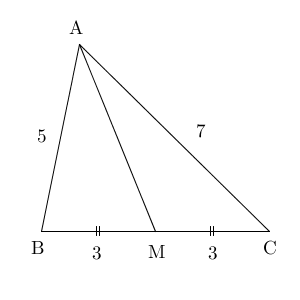
【標準】三角比と角の二等分線と同じようにして解くことができます。 AMを含む三角形 ABM と三角形 ABC を見比べると、 B が共通しています。余弦定理を用いて $\cos\angle \mathrm{ B }$ を2通りに書いて解くことができます。
まずは $\triangle \mathrm{ ABC }$ に着目して余弦定理を使うと
\begin{eqnarray}
\cos\angle \mathrm{ B }
&=&
\frac{5^2+6^2-7^2}{2\cdot 5\cdot 6} \\[5pt]
&=&
\frac{12}{2\cdot 5\cdot 6} \\[5pt]
&=&
\frac{1}{5} \\[5pt]
\end{eqnarray}となることがわかります。
続いて、 $\triangle \mathrm{ ABM }$ について余弦定理を使うと
\begin{eqnarray}
\mathrm{ AM }^2
&=&
5^2+3^2-2\cdot 5\cdot 3 \cdot \frac{1}{5} \\[5pt]
&=&
25+9-6 \\[5pt]
&=&
28 \\[5pt]
\end{eqnarray}となります。これから\[ \mathrm{ AM }=2\sqrt{7} \]と求められます。
別解
この例題は、別の解き方で解くこともできます。

ここで、 $\angle \mathrm{ B }$ ではなく、 $\angle \mathrm{ AMB }$, $\angle \mathrm{ AMC }$ について考えてみましょう。 $\mathrm{ AM }=m$ とすれば、余弦定理から m を使って $\cos$ の値を書くことができます。また、この2つの角度を足すと180度になることから、補角の公式が使えます。これらを組み合わせて解いてみましょう。
$\triangle \mathrm{ AMB }$ に対して余弦定理を使うと
\begin{eqnarray}
\cos\angle\mathrm{AMB}
&=&
\frac{3^2+m^2-5^2}{2\cdot 3\cdot m} \\[5pt]
&=&
\frac{m^2-16}{6m} \\
\end{eqnarray}となります。 $\triangle \mathrm{ AMC }$ に対して余弦定理を使うと
\begin{eqnarray}
\cos\angle\mathrm{AMC}
&=&
\frac{3^2+m^2-7^2}{2\cdot 3\cdot m} \\[5pt]
&=&
\frac{m^2-40}{6m} \\
\end{eqnarray}が得られます。補角の公式から\[ \cos\angle\mathrm{AMB}=-\cos\angle\mathrm{AMC} \]なので、
\begin{eqnarray}
\frac{m^2-16}{6m} &=& -\frac{m^2-40}{6m} \\[5pt]
m^2-16 &=& -(m^2-40) \\[5pt]
2m^2 &=& 56 \\[5pt]
m^2 &=& 28 \\[5pt]
\end{eqnarray}このことから、\[ \mathrm{ AM }=2\sqrt{7} \]と求められます。
なお、【標準】三角比と角の二等分線でも、この別解のやり方で解くこともできます。
おわりに
ここでは、三角比を用いて中線の長さを求める問題を考えました。角の二等分線の問題と同じように、辺の長さと余弦定理から $\cos$ がわかり、それを別の三角形に対して用いて他の辺の長さを求める、という方法で求められることを見ました。また、中線の場合には、同じ長さの辺を含んだ2つの三角形に対して余弦定理を使うことで、別の解き方ができることも見ました。
いろんな切り口で問題が解けるようになると、応用力もついてきます。どちらもマスターしておきましょう。





