【発展】三角比と中線定理
ここでは、【標準】三角比と中線で見た内容を一般化した「中線定理」についてみていきます。
中線定理
中線定理は次のような内容です。
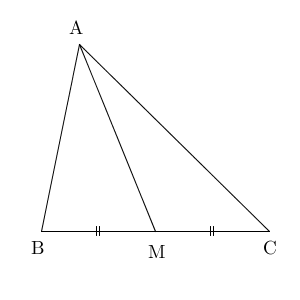
これがあれば、【標準】三角比と中線でみた例題は
\begin{eqnarray}
5^2+7^2 &=& 2(\mathrm{ AM }^2+3^2) \\
37 &=& \mathrm{ AM }^2+9 \\
\mathrm{ AM }^2 &=& 28
\end{eqnarray}となり、 $\mathrm{ AM } = 2\sqrt{7}$ が得られますね。
三角比を使った中線定理の証明
中線定理はいろいろな証明方法がありますが、ここでは三角比を用いて証明してみましょう。
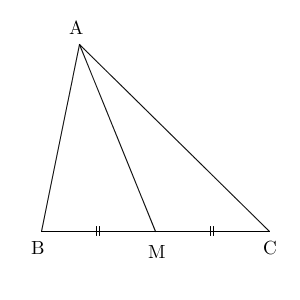
$\triangle \mathrm{ ABM }$ に対して余弦定理を使うと\[ \mathrm{ AB }^2=\mathrm{ AM }^2+\mathrm{ BM }^2-2\mathrm{ AM }\cdot\mathrm{ BM }\cos\angle \mathrm{ AMB } \]が得られます。また、 $\triangle \mathrm{ ACM }$ に対して余弦定理を使うと\[ \mathrm{ AC }^2=\mathrm{ AM }^2+\mathrm{ CM }^2-2\mathrm{ AM }\cdot\mathrm{ CM }\cos\angle \mathrm{ AMC } \]が得られます。
ここで、 $\mathrm{ BM }=\mathrm{ CM }$ であることと、補角の公式から $\cos\angle \mathrm{ AMC }=-\cos\angle \mathrm{ AMB }$ であることから、上の2つの式を足すと\[ \mathrm{ AB }^2 +\mathrm{ AC }^2 = 2(\mathrm{ AM }^2+\mathrm{ BM }^2) \]となり、中線定理が成り立つことがわかります。
おわりに
ここでは、三角比を使った中線定理の証明を紹介しました。中線定理を試験で使う場面はそれほど多くはありません。ただ、どのように証明すればいいかは理解しておくようにしましょう。三角比を使った証明の難易度はそれほど高くはないため、入試では自力で証明できるレベルになっておきたいですね。





