【標準】点の一致と位置ベクトル

🕒 2017/09/15 🔄 2024/07/06

ここでは、2つの点が一致することの証明に、位置ベクトルを使う方法を見ていきます。

📘 目次

この記事の内容の一部を以下の動画でも解説しています。

重心の存在と位置ベクトル

三角形 ABC があるとし、辺 BC, CA, AB の中点を、それぞれ、 P, Q, R とします。三角形 ABC の重心を G とします。

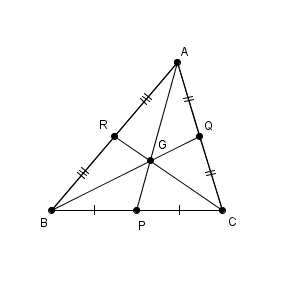
【基本】三角形の重心で見た通り、3つの中線、つまり、 AP, BQ, CR は重心 G で交わり、重心は中線を $2:1$ に内分するのでした。

上のリンク先で図形的な証明を考えていますが、2つの性質「3つの中線が1点で交わること」「重心は中線を $2:1$ に内分すること」は、どちらも自明なことではありません。2つの中線が1点で交わることは明らかですが、3つだと明らかではないですね。内分の比率も同様です。

この「1点で交わること」は、位置ベクトルを用いれば、スッキリと示すことができます。それぞれの中線を $2:1$ に内分する点の位置ベクトルを求めてみましょう。

A, B, C の位置ベクトルを、 $\vec{a}$, $\vec{b}$, $\vec{c}$ とします。このとき、 P, Q, R の位置ベクトルは、各辺の中点であることを使えば、順番に\[ \frac{\vec{b}+\vec{c} }{2}, \ \frac{\vec{c}+\vec{a} }{2}, \ \frac{\vec{a}+\vec{b} }{2} \]となります。よって、 AP を $2:1$ に内分する点の位置ベクトルは、【基本】内分点と外分点の位置ベクトルで見たように、
\begin{eqnarray} \frac{\vec{a}+2\times\dfrac{\vec{b}+\vec{c} }{2} }{3} = \frac{\vec{a}+\vec{b}+\vec{c} }{3} \end{eqnarray}となります。 BQ を $2:1$ に内分する点の位置ベクトルは \begin{eqnarray} \frac{\vec{b}+2\times\dfrac{\vec{c}+\vec{a} }{2} }{3} = \frac{\vec{a}+\vec{b}+\vec{c} }{3} \end{eqnarray}となり、 CR を $2:1$ に内分する点の位置ベクトルは \begin{eqnarray} \frac{\vec{c}+2\times\dfrac{\vec{a}+\vec{b} }{2} }{3} = \frac{\vec{a}+\vec{b}+\vec{c} }{3} \end{eqnarray}となります。3点とも、同じ位置ベクトルになります。

位置ベクトルが同じということは、対応する点の位置も同じ、ということです（参考：【基本】位置ベクトル）。そのため、3点は一致します。このことから、3つの中線が1点で交わることがわかります。

3つの中線が1点で交わることを示すために、「各中線を $2:1$ に内分する点」を調べました。1点で交わることを知らないのに、 $2:1$ に内分する点を調べればいい、と気づくことは不自然ですが、ここでは、「点が一致すること」を示すために、「位置ベクトルが一致すること」が役立つことがある、ということをおさえておきましょう。

点が一致することの証明

先ほどの三角形をもう一度見てみましょう。

ここで、三角形 PQR の重心が三角形 ABC の重心と一致することを示してみましょう。

先ほど見た通り、三角形 ABC の重心の位置ベクトルは\[ \frac{\vec{a}+\vec{b}+\vec{c} }{3} \]となるのでしたね。【基本】三角形の重心の位置ベクトルでも見た内容ですが、各頂点の位置ベクトルの平均が、重心の位置ベクトルとなります。そのため、三角形 PQR の重心の位置ベクトルは
\begin{eqnarray} & & \frac{1}{3}\left( \frac{\vec{a}+\vec{b} }{2} +\frac{\vec{b}+\vec{c} }{2} +\frac{\vec{c}+\vec{a} }{2} \right) \\[5pt] &=& \frac{1}{3} \times \frac{2\vec{a}+2\vec{b}+2\vec{c} }{2} \\[5pt] &=& \frac{\vec{a}+\vec{b}+\vec{c} }{3} \end{eqnarray}となります。2つの位置ベクトルが一致するので、2つの三角形の重心は一致することがわかります。

図形的に証明することもできますが、図は結構ごちゃごちゃしてきます。また、今回は、各辺の中点を結んだ三角形を考えましたが、各辺の内分点（各辺を $3:2$ に内分する点など）を結んだ三角形でも同じ結果が得られます。ベクトルなら係数が変わるだけですが、内分点バージョンを図で示すのは大変でしょう。