【応用】ベクトルの等式と三角形の面積比

🕒 2017/09/19 🔄 2024/07/06

ここでは、ベクトルの等式から三角形の面積比を求める問題を見ていきます。

📘 目次

ベクトルの等式

例題

$\triangle$ ABC の内部に点 P があり、 $3\overrightarrow{ \mathrm{ PA } }+4\overrightarrow{ \mathrm{ PB } }+5\overrightarrow{ \mathrm{ PC } }=\vec{0}$ を満たしている。このとき、面積比 $\triangle \mathrm{ PAB }:\triangle \mathrm{ PBC }:\triangle \mathrm{ PCA }$ を求めなさい。

この問題文のように、ベクトルの等式を使って点に関する条件が示されている場合があります。この扱いは、知っていれば簡単ですが、知らないと思いつくのは少し難しいです。

この条件は、 P が基準となっていますが、そもそも P はどこにある点かがわかりません。なので、ここを基準とするのはあまりよくありません。「基準を変える」という発想で、条件を変形していきましょう。

どれでもいいのですが、基準を A にしてみましょう。 $\overrightarrow{ \mathrm{ AP } }+\overrightarrow{ \mathrm{ PA } }=\vec{0}$, $\overrightarrow{ \mathrm{ AP } }+\overrightarrow{ \mathrm{ PB } }=\overrightarrow{ \mathrm{ AB } }$, $\overrightarrow{ \mathrm{ AP } }+\overrightarrow{ \mathrm{ PC } }=\overrightarrow{ \mathrm{ AC } }$ となることから、両辺に $12\overrightarrow{ \mathrm{ AP } }$ を足してみると、
\begin{eqnarray} 4\overrightarrow{ \mathrm{ AB } }+5\overrightarrow{ \mathrm{ AC } } &=& 12\overrightarrow{ \mathrm{ AP } } \\[5pt] \overrightarrow{ \mathrm{ AP } } &=& \frac{4\overrightarrow{ \mathrm{ AB } }+5\overrightarrow{ \mathrm{ AC } } }{12} \\[5pt] &=& \frac{3}{4} \cdot \frac{4\overrightarrow{ \mathrm{ AB } }+5\overrightarrow{ \mathrm{ AC } } }{9} \\[5pt] \end{eqnarray}と変形できます。

ここで、辺 BC を $5:4$ に内分する点を D とすると、上の式は\[ \overrightarrow{ \mathrm{ AP } }=\frac{3}{4}\overrightarrow{ \mathrm{ AD } } \]となります。よって、線分 AD を $3:1$ に内分する点が P だ、とわかります。

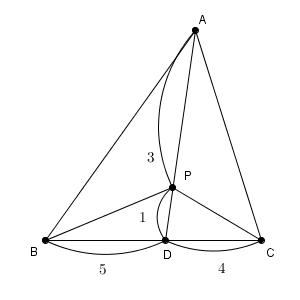
これで、ようやく、 P の位置がわかりました。あとは面積比を考えればおしまいですね。辺の比が分かっているので、面積比も求めることができます。

三角形 ABC の面積を S とすると、 $\mathrm{ BD }:\mathrm{ DC }=5:4$ なので、三角形 ABD の面積は $\dfrac{5}{9}S$ 、三角形 ACD の面積は $\dfrac{4}{9}S$ となります。

さらに、 $\mathrm{ AP }:\mathrm{ PD }=3:1$ なので、三角形 PAB の面積は\[ \frac{3}{4}\cdot\frac{5}{9}S=\frac{5}{12}S \]となり、三角形 PCA の面積は\[
\frac{3}{4}\cdot\frac{4}{9}S=\frac{1}{3}S \]となります。残りの部分が三角形 PBC なので、面積は\[ S-\frac{5}{12}S-\frac{1}{3}S=\frac{1}{4}S \]となります。

以上から、面積比は
\begin{eqnarray} & & \triangle \mathrm{ PAB }:\triangle \mathrm{ PBC }:\triangle \mathrm{ PCA } \\[5pt] &=& \frac{5}{12}S:\frac{1}{4}S:\frac{1}{3}S \\[5pt] &=& 5:3:4 \\[5pt] \end{eqnarray}となります。

係数と面積比を見て気づく人もいるかもしれませんが、一般的に、 $a\overrightarrow{ \mathrm{ PA } }+b\overrightarrow{ \mathrm{ PB } }+c\overrightarrow{ \mathrm{ PC } }=\vec{0}$ なら、 $\triangle \mathrm{ PBC }:\triangle \mathrm{ PCA }:\triangle \mathrm{ PAB }=a:b:c$ となります。