【基本】位置ベクトル

🕒 2017/09/11 🔄 2024/07/06

ここでは、平面上の点とベクトルとをつなぐ役割を持つ「位置ベクトル」について見ていきます。

📘 目次

位置ベクトルの導入

ベクトルというのは、向きと大きさを持ったものです（参考：【基本】ベクトル）。このベクトルを考えることで、基準を好きなところにして、軸も好きなものが使えるようになります（参考：【導入】ベクトルを考える意味について）。

座標では、原点を基準として、縦と横の方向を使うしかありませんでした。ベクトルの場合は、基準と軸を好きなように設定できるため、三角形や平行四辺形などの図形を扱うときには、考えやすくなるのでしたね（参考：【標準】ベクトルの内積と中線定理）。

ただ、毎回基準を選びたいというわけでもないんですよね。今までも $\overrightarrow{ \mathrm{ OA } }=\vec{a}$, $\overrightarrow{ \mathrm{ OB } }=\vec{b}$ などとおいてベクトルの問題を考えたことがありました。特に、座標平面上で図形を考える場合は、基準を原点にして、向きだけを自由に設定したい、ということが多いです。

そのため、基準を固定したベクトルを考えたい、という気持ちが出てきます。そこで出てくるのが「位置ベクトル」です。

位置ベクトル

平面上で、点 O を基準として固定します。このとき、平面上の点 P に対して、 $\overrightarrow{ \mathrm{ OP } }$ を「点 O に関する点 P の位置ベクトル(position vector)」と言います。

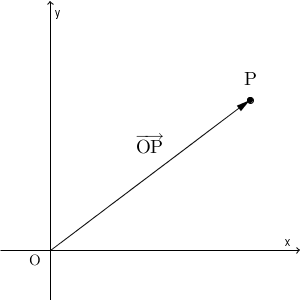
基準である点 O を固定しているので、終点を指定すればそれに対してベクトルが対応するので、それをその点の位置ベクトルと呼ぶわけですね。逆に、ベクトル $\vec{p}$ に対して、$\overrightarrow{ \mathrm{ OP } }=\vec{p}$ となる点 P が対応します。つまり、位置ベクトルは、点の位置と、ベクトルとを対応させるものなんですね。

点 P の位置ベクトルを $\vec{p}=\overrightarrow{ \mathrm{ OP } }$ で表すとき、これを記号で $\mathrm{ P }(\vec{p})$ と書きます。点と位置ベクトルとが対応している、ということがこの書き方にも表れていますね。

一般的に、位置ベクトルは、点のアルファベットを小文字にしたもので表すことが多いです。 $\mathrm{ A }(\vec{a})$ などという感じです。

また、普通、「位置ベクトル」と言った場合、点 O を基準としていることが多いです。

一般のベクトルと位置ベクトル

点 A, B の位置ベクトルを $\vec{a}$, $\vec{b}$ と表すとします。位置ベクトルの基準は O とします。

ベクトルを使うときには、 O 以外を基準とするベクトルを扱いたいこともあります。例えば、 $\overrightarrow{ \mathrm{ AB } }$ を扱いたい、という場合です。

この場合は、次のように変形すれば、位置ベクトルを用いて表すことができます。
\begin{eqnarray} \overrightarrow{ \mathrm{ AB } } &=& \overrightarrow{ \mathrm{ AO } }+\overrightarrow{ \mathrm{ OB } } \\[5pt] &=& \overrightarrow{ \mathrm{ OB } }-\overrightarrow{ \mathrm{ OA } } \\[5pt] &=& \vec{b}-\vec{a} \\[5pt] \end{eqnarray}このことから、どんなベクトルでも、位置ベクトルを用いて表すことができる、ということがわかります。

位置ベクトルが等しいとは

点 A, B の位置ベクトルを $\vec{a}$, $\vec{b}$ と表すとします。

もし、この2つの位置ベクトルが等しいならば、 $\overrightarrow{ \mathrm{ OA } }=\overrightarrow{ \mathrm{ OB } }$ が成り立ちます。 $\mathrm{O}$ から見た向きも距離も同じです。このことから、 A, B は同じ場所にある点だということがわかります。

位置ベクトルが同じなら、対応する点の位置も同じ。位置ベクトルがその点の位置を表しているのだから、当然ですね。