【標準】二次曲線と接線
ここでは、ある点から二次曲線に引いた接線の方程式を求める問題を見ていきます。
二次曲線と接線
接線を求める方法は、今までに何度か出てきました。例えば、【基本】微分と接線の方程式で見たように、微分を使う方法があります。微分を使えば、接点での傾きが簡単に得られます。しかし、楕円に対して微分を使う方法は、今はまだ難しいのでこの方法は使えません。
そこで、【標準】円に引いた接線の方程式で見た手法を応用します。「ある点から、ある曲線に引いた接線」と考えるのではなく、「ある点を通る直線が、ある曲線に接する」と考えるわけです。
【基本】二次曲線と直線で見たように、二次曲線と直線、2つの方程式を組み合わせれば、二次方程式ができます。そのため、接する条件も導くことができます。
これらを踏まえて考えていきましょう。
点 $(-1,1)$ を通る直線は、 $y=m(x+1)+1$ と書きたいところですが、一つ注意が必要です。この式では、傾きを m としていますが、前提として「 y 軸と平行ではない」ことを含んでしまっています。そもそも、 y 軸と平行な直線は解にならないことを確かめる必要があります。
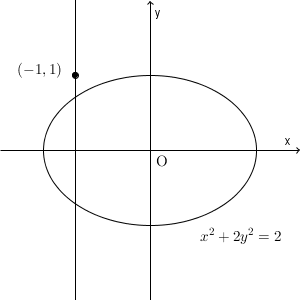
点 $(-1,1)$ を通り、 y 軸に平行な直線 $x=-1$ は、楕円と2点で交わるので、接線にはなりません。問題に答えるときにも、この確認は必要です。
さて、点 $(-1,1)$ を通り、 y 軸に平行ではない直線の傾きを $m$ とすると、この直線の方程式は\[ y=m(x+1)+1 \]と書くことができます。これと楕円との交点の x 座標は
\begin{eqnarray}
x^2+2(mx+m+1)^2 &=& 2 \\[5pt]
(2m^2+1)x^2+4m(m+1)x +2(m+1)^2-2 &=& 0 \\[5pt]
\end{eqnarray}の解となります。
よって、この直線と楕円が接するのは、判別式が $0$ となるときなので、
\begin{eqnarray}
\left\{4m(m+1)\right\}^2 -4(2m^2+1)\left\{2(m+1)^2-2\right\} &=& 0 \\[5pt]
2m^2(m+1)^2 -(2m^2+1)\left\{(m+1)^2-1\right\} &=& 0 \\[5pt]
2m^2(m+1)^2 -(2m^2+1)(m+1)^2 +(2m^2+1) &=& 0 \\[5pt]
-(m+1)^2 +(2m^2+1) &=& 0 \\[5pt]
m^2-2m &=& 0 \\[5pt]
m(m-2) &=& 0 \\[5pt]
m &=& 0,2 \\[5pt]
\end{eqnarray}となります。よって、直線の方程式に、この m の値を代入すれば、接線の方程式は、 $y=1$, $y=2x+3$ となることがわかります。これらが答えとなります。
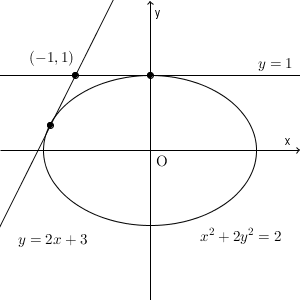
判別式が $0$ になる、という式を解くのが少し大変でしたね。将来的には、微分を使って解くこともできるようになりますが、それはまた別の機会に見ていくことにします。
おわりに
ここでは、ある点から二次曲線に引いた接線を求める方法を見てきました。楕円の例を挙げましたが、放物線や双曲線の場合も、考え方は同じです。ある点を通る直線の方程式と二次曲線の方程式を利用して二次方程式を作り、それが重解を持つときを考えましょう。





