【応用】二次曲線と離心率

ここでは、放物線、楕円、双曲線が互いに関連していることが理解できる、「離心率」について見ていきます。

双曲線と離心率

放物線は、焦点と準線からの距離が一定となる点の軌跡でした（参考：【基本】放物線の焦点と準線）。このように、ある点とある直線を使って、楕円や双曲線を得ることも可能です。以下でその例を見てみます。

点 P の座標を $(x,y)$ とします。

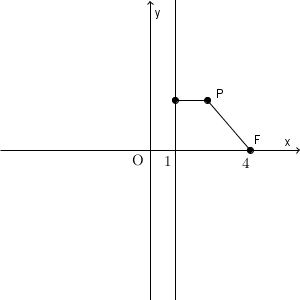
このとき、点 P と直線 $x=1$ との距離は $|x-1|$ であり、\[ \mathrm{ PF }^2=(x-4)^2+y^2 \]となります。よって、
\begin{eqnarray} (x-4)^2+y^2 &=& 4|x-1|^2\\[5pt] x^2-8x+16+y^2 &=& 4x^2-8x+4\\[5pt] -3x^2+y^2 &=& -12\\[5pt] \frac{x^2}{4}-\frac{y^2}{12} &=& 1\\[5pt] \end{eqnarray}となります。この計算を逆にたどっていくと、この双曲線上の点は、条件を満たすことがわかるので、求める軌跡は、\[ \frac{x^2}{4}-\frac{y^2}{12} = 1 \]となります。これが答えです。

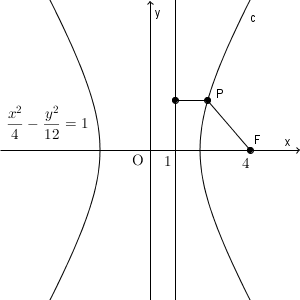
ちなみに、この双曲線の焦点は、 $(-4,0)$, $(4,0)$ となります（参考：【標準】双曲線の焦点）。つまり、問題文中にあった点 F が焦点となる、ということですね。

二次曲線と離心率

上で見た内容を、もう少し一般的な形で見てみましょう。

点 $\mathrm{ F }(c,0)$ からの距離と、直線 $x=-c$ からの距離の比が $e:1$ となる点 P の軌跡を求めます。ここで、 $c\gt 0$, $e\gt 0$ とします。

$e=1$ のときは、放物線ですね。以下では、 $e\ne 1$ のときを考えましょう。

点 P の座標を $(x,y)$ とすると、この点から直線 $x=-c$ との距離は $|x+c|$ となります。また、\[ \mathrm{ FP }^2=(x-c)^2+y^2 \]なので
\begin{eqnarray} (x-c)^2+y^2 &=& e^2|x+c|^2\\[5pt] x^2-2cx+c^2+y^2 &=& e^2x^2+2ce^2x+c^2e^2\\[5pt] (1-e^2)x^2-2c(1+e^2)x+y^2 &=& c^2(e^2-1)\\[5pt] \end{eqnarray}ここで、今、 $e^2\ne 1$ の場合を考えているので \begin{eqnarray} (1-e^2)\left(x-\frac{1+e^2}{1-e^2}c\right)^2+y^2 &=& c^2(e^2-1)+\frac{(1+e^2)^2}{1-e^2}c^2 \\[5pt] \left(x-\frac{1+e^2}{1-e^2}c\right)^2+\frac{y^2}{1-e^2} &=& \frac{4e^2}{(1-e^2)^2}c^2 \cdots (*) \\[5pt] \end{eqnarray}となります。

ここで、最後の式の右辺は正ですね。また、左辺の $x$ の係数も正です。なので、この曲線は、 $y$ の係数が正のとき、つまり、 $0\lt e\lt 1$ のときに楕円、 $y$ の係数が負のとき、つまり、 $e \gt 1$ のときに双曲線となります。（参考：【標準】二次曲線の標準化（平行移動によるもの））

最後の式は\[ x^2+\frac{y^2}{1-e^2} = \frac{4e^2}{(1-e^2)^2}c^2 \]を x 軸方向に $\dfrac{1+e^2}{1-e^2}c$ だけ平行移動したものです。 $0\lt e \lt 1$ のとき（楕円のとき）に、この式を $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$ となるように変形した場合、
\begin{eqnarray} a^2 &=& \frac{4e^2}{(1-e^2)^2}c^2 \\[5pt] b^2 &=& \frac{4e^2}{1-e^2}c^2 \\[5pt] \end{eqnarray}となります。よって、 \begin{eqnarray} & & -\sqrt{a^2-b^2} \\[5pt] &=& -\sqrt{\frac{4e^2}{(1-e^2)^2}c^2-\frac{4e^2}{1-e^2}c^2} \\[5pt] &=& -\frac{2ec}{1-e^2}\sqrt{1+(1-e^2)} \\[5pt] &=& -\frac{2e^2c}{1-e^2} \\[5pt] \end{eqnarray}となるので、(*)の焦点の1つの x 座標は \begin{eqnarray} -\frac{2e^2c}{1-e^2}+\dfrac{1+e^2}{1-e^2}c=c \end{eqnarray}となります。このことから、焦点の1つは、点 F と一致することがわかります。

また、 $e \gt 1$ のときも同様に計算すれば、焦点の1つが点 F になることがわかります。符号が少し変わるだけです。

このように、 e の値によって、軌跡が楕円、放物線、双曲線と変わっていきます。この e のことを、二次曲線の離心率(eccentricity) といいます。

なお、離心率 e を動かすと、次のように曲線が変化します。

おわりに

ここでは、離心率について見ました。試験などでは出題されることは少ないですが、二次曲線同士が関連していることを示す指標として重要な意味を持ちます。