🏠 Home / 数学A / 図形の性質 / 三角形の中心

【標準】三角形の垂心（なぜ3つの垂線は1点で交わるか）

🕒 2017/07/29 🔄 2023/05/01

ここでは、三角形の垂心が存在することを見ていきます。

📘 目次

垂線

三角形の垂心の話をする前に、垂線の話をします。

各頂点に対し、向かいにある辺（その頂点を含まない辺）のことを、対辺といいます。各頂点からは、次のように対辺に垂線を下ろすことができます。

対辺の延長線上に下ろすこともあります。

それぞれの頂点から垂線がひけるので、垂線は3本ひけることがわかります。

3つの垂線が1点で交わることの証明

この垂線について、次のような性質があります。

垂心の存在

三角形の各頂点から対辺にひいた3つの垂線は1点で交わる。

この点のことを垂心(orthocenter) といいます。このことを示してみましょう。なお、少し先で見ることになる、【基本】四角形が円に内接するための条件の結果を使います。

まずは名前をつけましょう。三角形 ABC において、 A, B から対辺に下した垂線の足をそれぞれ P, Q とします。この2つの線は平行にはならないので1点で交わります。この点を H とし、 CH と AB の交点を R とします。

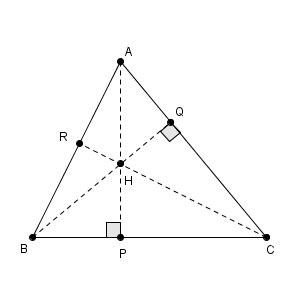
R のところには、直角マークがないことに注意しましょう。

この CR が垂線であることを示しましょう。もしこれが示せたら、3つの垂線は H で交わることがわかるからです。

$\angle \mathrm{ CPH }$, $\angle \mathrm{ CQH }$ はともに直角なので、 C, P, H, Q の4点は、 CH を直径とする円周上にあります。（参考：【基本】四角形が円に内接するための条件）

このことから、\[ \angle \mathrm{ HCQ }=\angle \mathrm{ HPQ } \]であることがわかります。

また、$\angle \mathrm{ APB }$, $\angle \mathrm{ AQB }$ もともに直角なので、 A, B, P, Q の4点は、 AB を直径とする円周上にあります。（参考：【基本】四角形が円に内接するための条件）

このことから、\[ \angle \mathrm{ APQ }=\angle \mathrm{ ABQ } \]であることがわかります。

よって、2つを合わせると\[ \angle \mathrm{ ACR }=\angle \mathrm{ ABQ } \]がわかります。このことから、
\begin{eqnarray} \angle \mathrm{ ARC } &=& 180^{\circ} -\angle \mathrm{ RAC } -\angle \mathrm{ ACR } \\[5pt] &=& 180^{\circ} -\angle \mathrm{ BAQ } -\angle \mathrm{ ABQ } \\[5pt] &=& \angle \mathrm{ AQB } \\[5pt] &=& 90^{\circ} \end{eqnarray}となることがわかります。つまり、 CR は AB に下した垂線であることがわかります。

鈍角三角形のときは、少し見た目が異なりますが、まったく同じように示すことができます。