【基本】四角形が円に内接するための条件

🕒 2022/08/27 🔄 2023/05/01

ここでは、四角形が円に内接するための条件を見ていきます。

📘 目次

円周角の定理の逆

【基本】円に内接する四角形では、四角形が円に内接するときには、対角の和が $180^{\circ}$ になることなどを見ました。

三角形は、必ず、ある円に内接します（参考：【基本】三角形の外心）が、四角形の場合はそうなるとは限りません。例えば、正方形ではないひし形の場合、円には内接しません。以下では、四角形がどのような条件を満たせば円に内接するか、を見ます。ネタバレをすると、「対角の和が $180^{\circ}$」なら円に内接します。つまり、上のリンク先で見た「円に内接する四角形」の性質を持っていたら、その四角形は円に内接する、ということです。

このことを示すために、円周角の定理の逆を使うので、どのような内容だったか復習しておきましょう。中学で学ぶ内容です。

円周角の定理の逆

4点 $\mathrm{A, B, P, Q}$ について、点 $\mathrm{P, Q}$ が直線 $\mathrm{AB}$ に関して同じ側にあって、 $\angle\mathrm{APB}=\angle \mathrm{AQB}$ を満たすならば、4点 $\mathrm{A, B, P, Q}$ は同一円周上にある。

ちなみに、「点 $\mathrm{P, Q}$ が直線 $\mathrm{AB}$ に関して同じ側にある」という条件がありますが、これは必要です。例えば、以下の図のようなケースを考えてみましょう。

これは、正三角形を2つ並べたもので、 $\angle\mathrm{APB}=\angle \mathrm{AQB}$ を満たしますが、4点が同一円周上にはありません。このように、直線 $\mathrm{AB}$ について、点 $\mathrm{P}$ と点 $\mathrm{Q}$ が異なる側にある場合は成り立たないこともあります。「点 $\mathrm{P, Q}$ が直線 $\mathrm{AB}$ に関して同じ側にある」という条件は忘れないようにしましょう。

四角形が円に内接するための条件

四角形が円に内接するためには、以下の条件を満たせばいいです。

四角形が円に内接するための条件

次の 1. または 2. が成り立つ四角形は、円に内接する。
1. 対角の和が $180^{\circ}$ である。
2. 内角が、その対角の外角に等しい。

【基本】円に内接する四角形では、円に内接するときに上で挙げた性質を持つことを見ましたが、逆にこれらの性質を持っていればその四角形は円に内接することが言える、という内容です。以下では、この内容を示していきます。

四角形 $\mathrm{ABCD}$ において、\[ \angle \mathrm{B}+\angle \mathrm{ADC}=180^{\circ} \quad\cdots ① \]とします。

4つの頂点を通る円が存在するかどうかはわかりませんが、3つの頂点を通る円は必ず存在します。そこで、 $\triangle \mathrm{ABC}$ の外接円を考えます。この外接円を円 $\mathrm{O}$ とします。また、 $\mathrm{B}$ を含まない弧 $\mathrm{AC}$ 上に点 $\mathrm{E}$ をとります。円 $\mathrm{O}$ は $\triangle \mathrm{ACE}$ の外接円ともいえます。

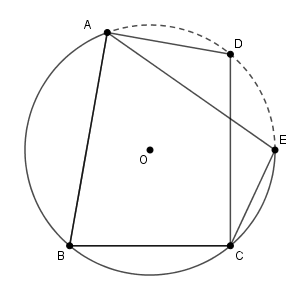
（$\mathrm{D}$ はこの時点ではまだ同一円周上にあるかどうかわからないので、$\mathrm{D}$ のまわりの弧は破線にしています。）

このとき、四角形 $\mathrm{ABCE}$ は円 $\mathrm{O}$ に内接するので、\[ \angle \mathrm{B}+\angle \mathrm{AEC}=180^{\circ} \quad\cdots ② \]が成り立ちます。これは円に内接する四角形の性質ですね。

① と ② から\[ \angle \mathrm{ADC}=\angle \mathrm{AEC} \]となります。 $\mathrm{D, E}$ は直線 $\mathrm{AC}$ に関して同じ側にあるので、円周角の定理の逆から、4点 $\mathrm{A,C,D,E}$ は同一円周上にあります。

ここまでくれば、示せたも同然です。点 $\mathrm{B}$ も、点 $\mathrm{D}$ も、 $\triangle \mathrm{ACE}$ の外接円上にあることがわかったので、4点 $\mathrm{A,B,C,D}$ は同一円周上にあること、四角形 $\mathrm{ABCD}$ が円に内接することがいえました。

2. の「内角が、その対角の外角に等しい」が成り立つとき、1.の「対角の和が $180^{\circ}$ である」ことがいえるので、2. が成り立つときにも四角形が円に内接することがいえます。

例題

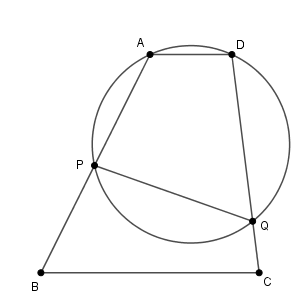
次の図で、線分 $\mathrm{AD}$ と線分 $\mathrm{BC}$ は平行です。このとき、四角形 $\mathrm{PBCQ}$ が円に内接することを示しなさい。

まず、線分 $\mathrm{AD}$ と線分 $\mathrm{BC}$ が平行なので、\[ \angle \mathrm{A}+\angle \mathrm{B}=180^{\circ} \]です。また、四角形 $\mathrm{APQD}$ が円に内接しているので、\[ \angle \mathrm{A}=\angle \mathrm{PQC} \]が成り立ちます。

以上から、\[ \angle \mathrm{PQC}+\angle \mathrm{B}=180^{\circ} \]となるので、四角形 $\mathrm{PBCQ}$ が円に内接することがわかります。

なお、この問題では「四角形 $\mathrm{PBCQ}$ が円に内接することを示しなさい」となっていますが、「4点 $\mathrm{P,B,C,Q}$ が同一円周上にあることを示しなさい」と問われることもあります。聞かれ方が違っても、やるべきことは同じです。