【標準】比例のグラフ
ここでは、比例のグラフに関する問題を見ていきます。
座標に関する問題
比例のグラフに関する問題の前に、まずは座標に関する問題を見てみましょう。
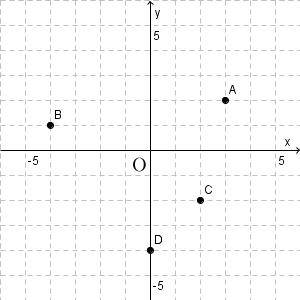
【基本】比例のグラフで見ましたが、座標は、 $(a,b)$ というように、 $x$ 座標、 $y$ 座標を並べて書きます。 $x$ 座標は、原点から右にどれだけ進んだ点かを表していて、 $y$ 座標は、上にどれだけ進んだ点かを表しています。
点 A は、原点から右に3、上に2だけ移動した点です。なので、点 A の座標は、 $(3,2)$ であることがわかります。点 B は原点より左にあるので、 $x$ 座標は負の数となります。座標は $(-4,1)$ となります。
点 C は、原点より下にあるので、 $y$ 座標が負となり、座標は $(2,-2)$ となります。点 D は、 $y$ 軸上の点なので、原点から左右に移動しなくてもいいため、 $x$ 座標は $0$ となります。座標は $(0,-4)$ となります。
比例のグラフをかく問題
(1) $y=-2x$
(2) $y=\dfrac{1}{3}x$
【基本】比例のグラフの性質の最後で見たように、比例のグラフは原点を通る直線になります。よって、原点以外に通る点がわかれば、グラフをかくことができます。
(1)の場合は、 $x=1$ とすると $y=-2$ となるため、点 $(1,-2)$ を通ることがわかります。よって、原点とこの点を結んだ直線が答えとなります。
(2)の場合は、 $x=1$ としても $y=\dfrac{1}{3}$ となり、点を選ぶことが難しいです。こういう場合は、 $y$ 座標が整数となるように $x$ をうまく選べばいいです。今の場合なら、 $x=3$ とすればいいですね。このとき、 $y=1$ となるので、 $(3,1)$ を通ることがわかります。
以上から、2つのグラフは次のようになります。

比例のグラフから式を求める問題

比例の式を求めるので、 $y=ax$ の $a$ を求めればいいですね。
(1)は、原点を通り、点 $(1,1)$ を通る直線なので、 $y=ax$ に $x=1$, $y=1$ を代入すると、 $a=1$ だとわかります。よって、 $y=x$ となります。
(2)は、原点以外に通る点のうち、 $x$ 座標も $y$ 座標も整数になっている点を見つけましょう。そうすると、点 $(3,-4)$ が見つかります。これらを $y=ax$ に代入すると $-4=3a$ となるので、 $a=-\dfrac{4}{3}$ となることがわかります。よって、式は、 $y=-\dfrac{4}{3}x$ となります。
なお、原点を通る直線は、必ず比例のグラフになります。原点以外に点 $(m,n)$ を通るとすると、 $y=\dfrac{n}{m}x$ のグラフは原点を通る直線になるので、この直線は $y=\dfrac{n}{m}x$ という比例の式に対応するグラフになります。
比例のグラフと変域
最後に、【標準】比例を表す式で見た問題を、グラフを用いて考えてみましょう。
(1) $y=3x$ で、 $x$ の変域が $-4\leqq x \leqq 5$ のとき、 $y$ の変域を答えなさい。
(2) $y=-5x$ で、 $x$ の変域が $1\lt x \lt 3$ のとき、 $y$ の変域を答えなさい。
この問題は、グラフをかく必要はありませんが、グラフで考えると次のようになります。
まず、 $y=3x$ のグラフをかいてみます。 $x$ の変域をいったん無視してグラフをかくと、 $(1,3)$ と原点とを結ぶ直線となります。
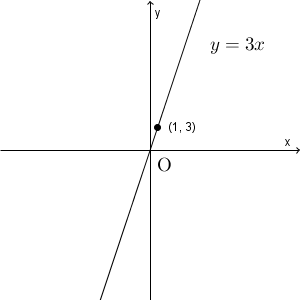
次に、変域も考慮しましょう。 $x$ の変域が $-4\leqq x \leqq 5$ ということは、横方向について、 $-4$ から $5$ までの部分を考えるということです。対応する $y$ 座標を追加すると、次のようになります。

$y$ の変域とは、上下方向にどのような値をとるかを表したものです。なので、この図から、 $-12\leqq y \leqq 15$ となることがわかります。右肩上がりのグラフなので、 $x$ が大きくなるほど $y$ も大きくなることが視覚的にわかります。
なお、線の端を含むことを強調して示したい場合は、上のように黒丸を使います。
(2)も同じようにグラフで考えてみましょう。 $y=-5x$ は、 $(1,-5)$ と原点とを結んだものがグラフとなります。
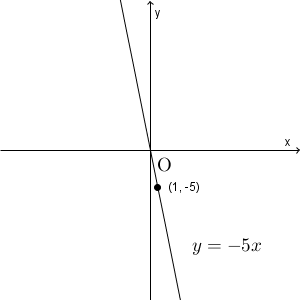
$1\lt x \lt 3$ の変域で考えると、次のようになります。今回は、端を含みません。含まないことを示したい場合は、白丸で使います。

このことから、 $y$ の変域は、 $-15\lt y \lt -5$ となることがわかります。右肩下がりのグラフなので、 $x$ が大きくなるほど $y$ は小さくなります。
おわりに
ここでは、比例のグラフに関連する問題を見てきました。原点と他の1点を通る直線であることがわかっているので、グラフをかくのはそれほど大変ではないでしょう。





