【基本】比例のグラフの性質
ここでは、比例のグラフを復習した後に、比例のグラフの性質を見ていきます。
比例のグラフの復習
【基本】比例のグラフで比例のグラフのかきかたを見ましたが、ここでは、別の比例のグラフをかいてみましょう。
$y=-2x$ のグラフをかいてみます。グラフをかくには、点をつないでいけばいいので、まずはいくつかの点の座標を求めます。値の対応表をかくと、次のようになります。
| $x$ | $y$ |
|---|---|
| -3 | 6 |
| -2 | 4 |
| -1 | 2 |
| 0 | 0 |
| 1 | -2 |
| 2 | -4 |
| 3 | -6 |
これをもとに、対応する点をとると、次のようになります。

さらに点をとる間隔を狭めてたくさんの点をとっていくと、次のようになります。

これが $y=-2x$ のグラフになります。
上のリンク先で見た $y=2x$ のグラフと見比べてみましょう。
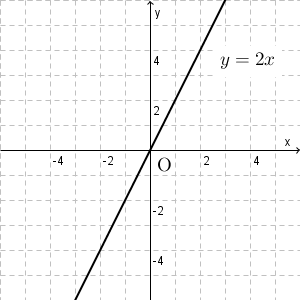
共通しているところと違うところがありますね。見比べて考えてみましょう。
まず、共通している部分は、どちらもグラフが直線になっている点です。そして、どちらの直線も、原点を通っていますね。
一方、 $y=2x$ のグラフは、右肩上がりの直線であるのに対し、 $y=-2x$ のグラフは右肩下がりになっている点がことなります。
どうしてこれらの性質を持つのか、以降で詳しく見てみましょう。
xの値が増加したときのyの値の変化
比例の式 $y=ax$ で、 $x$ の値が増加したときの $y$ の値について考えてみます。
まず、 $x=0$ とすると、 $y=0$ となります。これは、比例定数 $a$ がどんなときにも成り立ちます。なので、比例のグラフは、必ず原点を通ることがわかります。
次に、 $y=2x$ と $y=-2x$ を使って、 $x$ を増やしていったときの $y$ の変化を考えてみましょう。
$y=2x$ のときは、 $x$ に正の数を掛けたものが $y$ なので、 $x$ が増えれば増えるほど、 $y$ も増えていくことがわかります。つまり、グラフでは、原点から右に行くにつれて、上に移動していくことがわかります。
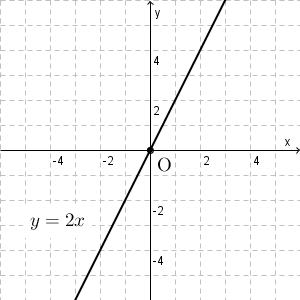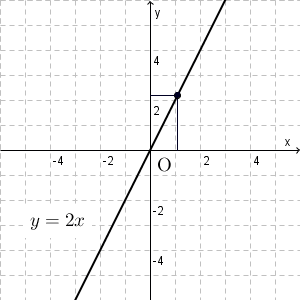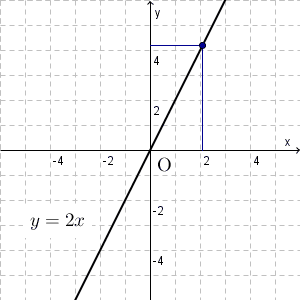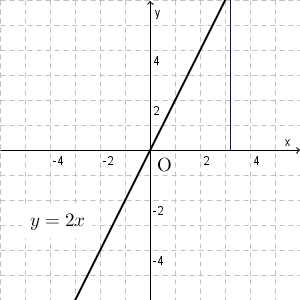
このことから、グラフは右肩上がりになることがわかります。
一方、 $y=-2x$ のときは、 $x$ に負の数を掛けたものが $y$ なので、 $x$ が増えれば増えるほど、 $y$ は減っていくことがわかります。つまり、グラフでは、原点から右に行くにつれて、下に移動していくことがわかります。
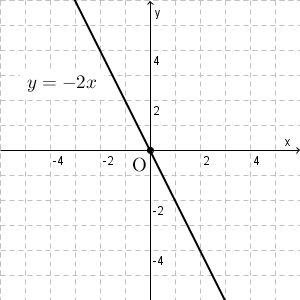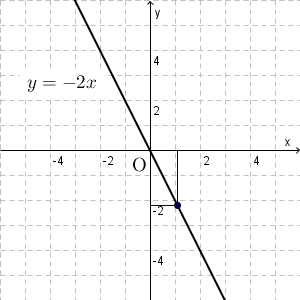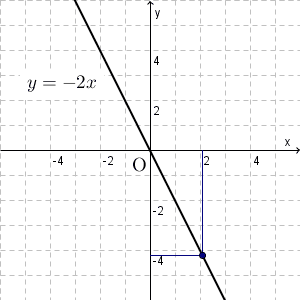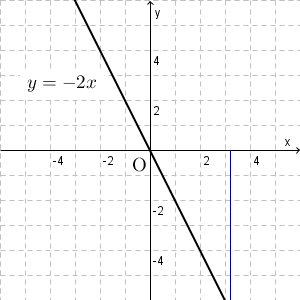
このことから、グラフは右肩下がりになることがわかります。
$x$ に掛かっている数、つまり、比例定数が、正か負かによって、グラフが右肩上がりになるか右肩下がりになるかが決まるということですね。 $y=ax$ のグラフは、 $a\gt 0$ なら右肩上がり、 $a\lt 0$ なら右肩下がりになることがわかります。
xの値が1だけ増加したときのyの値の変化
$x$ が増えたときに $y$ が増えるか減るかは、比例定数の符号によって決まることがわかりました。実は、それだけでなく、増え方や減り方にも特徴があります。
$y=2x$ について考えてみます。このとき、 $x$ の値が $1$ だけ増えると $y$ はどう変わるでしょうか。例えば、 $x=3$ から $x=4$ に変化したとき、 $y$ はどれだけ変化するでしょう。 $x=0$ から $x=1$ のときや、 $x=-2$ から $x=-1$ のときなども考えてみましょう。
計算してみるとわかりますが、 $y$ は、つねに $2$ だけ増えることがわかります。もし、 $x=m$ から $x=m+1$ に増えたときであれば、\[ 2(m+1)-2m=2 \]となるので、 $m$ に関係なく、 $y$ は $2$ 増えることがわかります。
一般に、 $y=ax$ のとき、 $x=m$ から $x=m+1$ に増えるとすると、\[ a(m+1)-am=a \]となるので、 $m$ に関係なく、 $y$ は $a$ だけ変化することがわかります。
これは、比例のグラフでは、場所に関係なく $x$ を $1$ だけ増やせば、 $y$ は $a$ だけ変化する、ということを表しています。
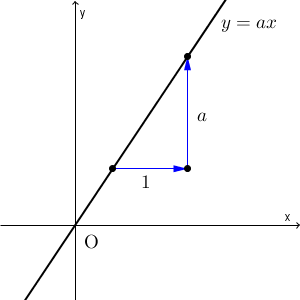
つまり、変化のしかたが一定である、ということです。そのため、比例のグラフは、必ず直線になります。
比例のグラフの性質
以上のことをまとめると、次のようになります。
比例定数 $a$ が正なら、右肩上がりの直線となり、 $a$ が負なら、右肩下がりの直線となる。
直線は、2つの点を決めれば1つに決まります。原点を通ることがわかっているので、比例のグラフをかくためには、原点以外に通る1点がわかればいいです。
今まで、たくさんの点をとってつないでグラフをかいていましたが、その必要はありません。 $y=2x$ のグラフなら、原点と点 $(1,2)$ とを結べばOKです。 $y=-2x$ なら、原点と点 $(1,-2)$ とを結んだ直線がグラフとなります。
おわりに
ここでは、比例のグラフの性質を見てきました。原点を通る直線になること、比例定数の符号によって、右肩上がりかどうかが決まることをおさえておきましょう。また、原点以外に通る1点を見つければ、グラフがかけることも理解しておきましょう。





