【基本】比例のグラフ

ここでは、比例のグラフのかきかたを見ていきます。

座標平面

$y=2x$ のように、 $y=ax$ という関係式が成り立っているとき、 $y$ は $x$ に比例するというのでした。このときの値の対応は、【基本】比例の性質で見たように、表を利用して確かめることができます。

しかし、もっと視覚的にわかりやすい、グラフを使う方法もあります。以下では、グラフを使って、比例の関係を図形的に把握する方法を見ていきます。

グラフは、小学校でも使っていたと思いますが、中学のグラフは少し違うところがあります。今後は、グラフは次のような平面にかきます。

負の数を学んだので、負の数も表せるようになっている点が大きく異なります。横に伸びる基準の線を $x$ 軸や横軸と言います。縦に伸びる基準線を $y$ 軸や縦軸と言います。二つの軸を合わせて、座標軸と言います。右・上が正の向きです。

また、座標軸の交点は原点と呼び、アルファベットの $\mathrm{O}$ で表します。このような平面のことを座標平面といいます。数直線は左右に伸びる線でした（参考：【基本】正負の数と大小）が、座標平面は上下左右に広がる平面です。

座標平面上の点

比例の式 $y=2x$ であれば、例えば、 $x=1$ のときに $y=2$ となります。このような数字のペアと座標平面上の点とを次のように対応します。

まず、原点を出発点として、 $x$ 軸にそって $1$ 進み、 $y$ 軸にそって $2$ 進みます。こうして到達する点を、 $x=1$, $y=2$ に対応させます。

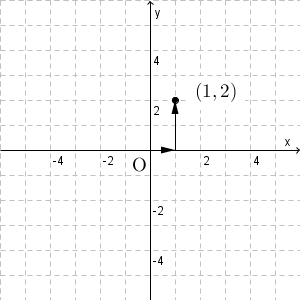
座標平面上の点がどこにあるかを表すものを座標といい、 $(1,2)$ と表します。1つ目の数字を $x$ 座標、2つ目を $y$ 座標といいます。原点から、横にどれだけ、縦にどれだけ移動するかをまとめて、丸カッコでくくったものが座標です。

逆に、座標平面上の点から座標を把握するには、 $x$ 軸、 $y$ 軸に垂線をおろして、軸との交点の数字を見ます。

上の図の点P であれば、 $x$ 座標が $-2$ で $y$ 座標が $3$ であることがわかります。よって、点 P の座標は $(-2,3)$ とかきます。点 $\mathrm{ P }(-2,3)$ と書いて、点と座標をまとめることもあります。

原点 O の座標は $(0,0)$ です。原点から右に $1$ だけ移動した点は $(1,0)$ となります。このように $x$ 座標や $y$ 座標が $0$ になることもあります。

比例のグラフ

座標平面上での点について見てきましたが、今度は比例のグラフについて考えてみます。

$y=2x$ について考えてみましょう。値の対応表をかくと、次のようになります。

$x$	$y$
-3	-6
-2	-4
-1	-2
0	0
1	2
2	4
3	6

これらに対応する点をとっていってみましょう。つまり、 $x=1$ のときに $y=2$ となるのだから、座標平面上の点 $(1,2)$ に印をつける、ということです。上の7つのペアを座標平面上に追加すると、次のようになります。

飛び飛びですが、この間がどうなっているかは、対応する点をどんどん埋めていけばいいですね。例えば、 $x=\dfrac{1}{2}$ や $x=\dfrac{1}{4}$ などの場合を考え、計算して点を追加していくと、次のような直線になることがわかります。

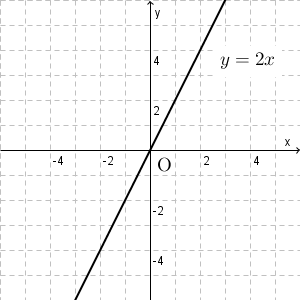
これが、比例のグラフです。グラフとは、2つの値の関係（ここでは $x$ と $y$ のこと）を、平面上の点の集まりとして、視覚的にあらわしたもののことです。

いくつかの代表的な点をとってつないでいけば、比例のグラフが得られます。小学校のときに見た比例のグラフは、右上の部分だけでしたが、負の数を学んだ後は、左下にも直線が伸びている点に注意しましょう。

おわりに

ここでは、比例のグラフについて見てきました。今後、いろんなグラフをかいていくことになりますが、グラフの基本的な項目についても合わせて見てきました。たくさん点をとって、どのようなグラフになるか考えるというのは、今後もいろいろなグラフをかく上で重要な手法です。