【標準】微分を利用して2つの放物線の共通接線を求める
ここでは、2つの放物線の共通接線を求める問題を見ていきます。まずは、微分を使わない方法、続いて、微分を使う方法、と見ていきます。
2つの放物線の共通接線
共通接線というのは、両方に接する接線、ということです。
まずは、二次関数の問題だと思って考えてみましょう。
求める接線の方程式を $y=mx+n$ とおきます。これが $y=x^2-6x+5$ に接するということから、「右辺同士が等しい」とおいた方程式は、重解を持ちます(参考:【標準】二次関数のグラフと直線との共有点)。つまり、
\begin{eqnarray}
x^2-6x+5 &=& mx+n \\[5pt]
x^2-(6+m)x+5-n &=& 0 \\[5pt]
\end{eqnarray}が重解を持つので、判別式が $0$ になる、ということです。よって、
\begin{eqnarray}
(m+6)^2 -4(5-n) &=& 0 \\[5pt]
m^2+12m+36 -20+4n &=& 0 \\[5pt]
m^2+12m+4n+16 &=& 0 \\[5pt]
\end{eqnarray}が成り立ちます。
また、この直線は $y=-x^2$ とも接するので
\begin{eqnarray}
-x^2 &=& mx+n \\[5pt]
x^2+mx+n &=& 0 \\[5pt]
\end{eqnarray}は重解を持ち、判別式が $0$ となるので
\begin{eqnarray}
m^2-4n &=& 0
\end{eqnarray}が成り立ちます。
この2つを同時に満たす $m,n$ を求めればいいですね。2つの式を辺々足すと、 $n$ が消え、次のように計算できます。
\begin{eqnarray}
2m^2+12m+16 &=& 0 \\[5pt]
m^2+6m+8 &=& 0 \\[5pt]
(m+2)(m+4) &=& 0 \\[5pt]
m &=& -2,-4 \\[5pt]
\end{eqnarray}これらを2つ目の式 $m^2-4n=0$ に代入すれば、 $m=-2$ のときは $n=1$ 、 $m=-4$ のときは $n=4$ となることがわかります。
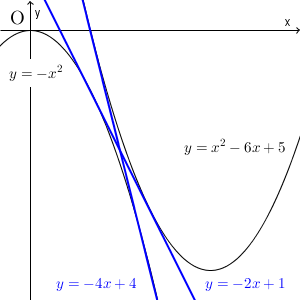
以上から、求める方程式は $y=-2x+1$, $y=-4x+4$ となることがわかります。
微分を利用して解く
上のように、「接する⇒判別式が $0$ 」と考えてもいいのですが、微分を使って解く方法も見ておきましょう。
微分を使って接線について考える場合は、接点を文字で置くほうが考えやすいことが多いです(参考:【標準】三次関数の接線の傾きから接線を求める)。ここでも、接点を文字で置いて考えていきましょう。
2つ目の二次関数の方がシンプルなので、こちらを基準に考えましょう。まず、放物線 $y=-x^2$ の $(a,-a^2)$ での接線の方程式を求めます(参考:【基本】微分と接線の方程式)。 $y=-x^2$ を微分すると $y'=-2x$ なので、接線の方程式は
\begin{eqnarray}
y-(-a^2) &=& -2a(x-a) \\[5pt]
y &=& -2ax +2a^2-a^2 \\[5pt]
&=& -2ax +a^2 \\[5pt]
\end{eqnarray}となることがわかります。これが $y=x^2-6x+5$ にも接する、と考えます。ここでさらに別の接点を文字で置いて考えることもできますが、この段階では、「接する⇒判別式が $0$ 」を使う方がいいです。そうすれば、文字が1つだけのまま(つまり、 a だけしか使わない)で解くことができるからです。
$y=-2ax+a^2$ が $y=x^2-6x+5$ に接する、ということは、右辺同士が等しい、とおいた式が重解を持ち、判別式が $0$ になる、ということなので、
\begin{eqnarray}
-2ax+a^2 &=& x^2-6x+5 \\[5pt]
x^2+(2a-6)x-a^2+5 &=& 0 \\[5pt]
\end{eqnarray}の判別式が $0$ になることから
\begin{eqnarray}
(2a-6)^2 -4(-a^2+5) &=& 0 \\[5pt]
(a-3)^2 -(-a^2+5) &=& 0 \\[5pt]
a^2-6a+9 +a^2-5 &=& 0 \\[5pt]
2a^2-6a+4 &=& 0 \\[5pt]
a^2-3a+2 &=& 0 \\[5pt]
(a-1)(a-2) &=& 0 \\[5pt]
a &=& 1,2 \\[5pt]
\end{eqnarray}となります。接線の方程式は $y=-2ax+a^2$ なので、これに代入すれば答えになります。よって、求める方程式は、 $y=-2x+1$ と $y=-4x+4$ となります。

当たり前ですが、1つ目の解き方と答えは同じですね。1つ目の方法は、「直線が、1つ目の放物線にも2つ目の放物線にも接する」という考え方です。2つ目の方法は、「2つ目の放物線の接線が、1つ目の放物線に接する」という考え方です。また、「接する」を「判別式が $0$ 」と言い換えて解いています。
どちらで解いても計算量はそれほど変わらないかもしれませんが、個人的には、微分を使うと「2つ目の放物線の接線」だけはすぐに出せるので、微分を使って解けるならこちらを選んだほうがいいのではないか、と思います。
おわりに
ここでは、2つの放物線の共通接線を求める方法を見ました。微分を使わない方法と微分を使う方法を見ました。どちらの解き方でも構いませんが、両方ともできるようになっておいたほうがいいでしょう。





