【導入】文字式の計算

ここでは、マッチ棒で正方形を作る問題を振り返りながら、文字式の計算がなぜ必要かを考えていきます。

正方形を作るのにマッチ棒は何本必要か（再び）

【基本】文字を使った式で表そうで見た問題をもう一度考えてみましょう。

マッチ棒を使って、次のように横につながった正方形をいくつか作っていきます。正方形の縦の長さがマッチ棒1本分の長さです。

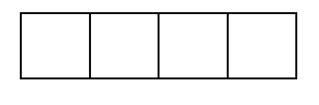
正方形を $x$ 個作る場合に、何本マッチ棒が必要かを考えてみます。いきなり考えるのは難しいので、まずは、規則性を見つけるため、正方形が少ない場合で考えるといいのでしたね。

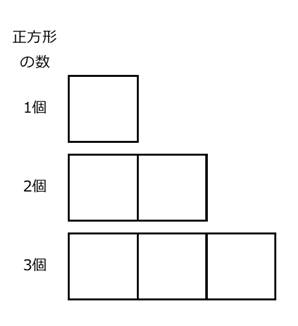
上にようにかいて直接数えてみると、正方形が1個、2個、3個となるにつれ、マッチ棒の数は4本、7本、10本となっていきます。3本ずつ増えていますね。

この3本はどこからきているのでしょう。それは、正方形が増えたときに、マッチ棒のどの部分が変わったかに着目すればいいですね。正方形が増えるごとに、右側にある「コ」の字の部分が増えています。なので、この図形を、「コ」の字の部分で分けて考えてみると、わかりやすくなります。

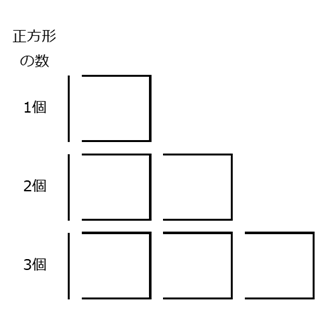
こうすると、左端にある1本と、右側にある「コ」の字にわけて数えられることがわかります。「コ」の個数は、正方形の個数と同じなので、必要なマッチ棒の数は、\[ 1+3\times x=1+3x \]本である、とわかります。

マッチ棒の数え方は一通りではない

先ほどは、正方形を、「｜」と「コ」の形に分けて、マッチ棒の本数を数えました。しかし、マッチ棒の数え方、正方形の分割の仕方は、これだけではありません。

例えば、次のように分割することもできるでしょう。

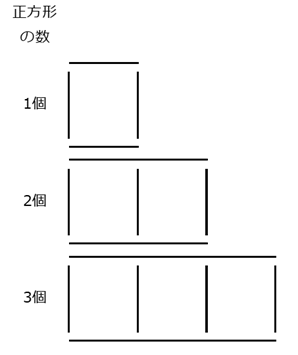
これは、正方形の上側の辺、下側の辺、そして、左右に並んでいる辺に分解する、という数え方です。正方形が $x$ 個のとき、上側にあるマッチ棒の数は、 $x$ 本ですね。下側にも $x$ 本あります。左右に並んでいる数は、規則性から、正方形の数より1本多いことがわかるので、このように分解すると\[ x+x+(x+1) \]本である、と考えられます。

さらに、次のような分割の仕方もあるでしょう。

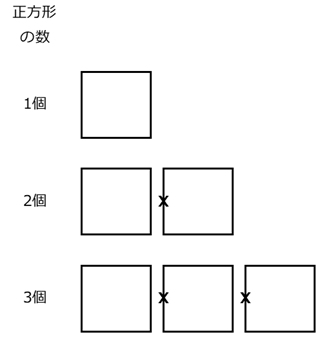
これは、まず独立した（横につながっていない）正方形を $x$ 個作り、共有する辺（上の図の「×」の辺）の数を後から抜く、という発想です。独立した正方形を $x$ 個作るには、 $4\times x$ 本のマッチ棒が必要ですね。また、この独立した $x$ 個の正方形をくっつける場合、取り除くマッチ棒の数は、正方形の数より1つ少ない、 $(x-1)$ 本であることが、規則性からわかります。ということは、このような分割方法だと\[ 4x-(x-1) \]本である、となります。

文字式の計算

先ほどは、いろいろなマッチ棒の数え方を見てきました。もちろん、どのように分割して数えても、正しく式が作られているなら、答えは同じになるはずです。なので、ここで導いた3つの式、 $1+3x$, $x+x+(x+1)$, $4x-(x-1)$ はどれも同じものになります。

例えば、 $x=10$ としてみましょう。1つ目の式は $1+3\times 10=31$ となります。2つ目の式は、 $10+10+(10+1)=31$ となります。3つ目の式は、 $4\times 10-(10-1)=31$ となります。3つとも $31$ となり、確かに同じ値になります。

ただ、3つの式は見た目が違うので、同じ内容だということがわかりにくいですね。なので、同じ内容だとわかりやすいように、見た目を変えることができると嬉しいです。

先ほど挙げた3つの式、 $1+3x$, $x+x+(x+1)$, $4x-(x-1)$ をよく見ると、1つ目が一番短いです。先ほど、 $x=10$ を代入しましたが、1つ目の式は1回の代入で済むのに、2つ目と3つ目は代入する回数が多いですね。なので、1つ目が一番シンプルだと言えるでしょう。

実は、2つ目の式も3つ目の式も、1つ目の式の形に変えることができます。このように、式の見た目を簡単にすることを、「式（文字式）を計算する」といいます。今後、文字式の計算の仕方を見ていくことになります。

おわりに

ここでは、文字式の計算がなぜ必要かを見てきました。マッチ棒の数え方によって、式の見た目が変わりました。同じものを表しているのに、見た目が違うのは不便ですね。なので、シンプルな形に変形すると便利です。このように、シンプルな形にする「式の計算」は、今後数学を学んでいく上でとても重要なものとなります。これから学んでいきましょう。