【導入】方程式

🕒 2019/05/16 🔄 2023/05/01

ここでは、ある具体的な状況をもとに、方程式について見ていくことにします。いろんな内容を一気に駆け抜けているので少し難しいかもしれませんが、はじめは雰囲気を感じ取るだけでも構いません。細かな内容は、別のページで順を追って説明していきます。

📘 目次

ケーキの値段を考えよう

次のような状況を考えてみましょう。

例題

Ａさんは、ある店でチョコレートケーキとチーズケーキを合わせて10個買う場合の、合計金額を試算してみた。すると、チョコレートケーキを7個買う場合の合計金額は、3個買う場合の合計金額よりも、200円高くなることがわかった。
チョコレートケーキが320円だとすると、チーズケーキはいくらだろうか。

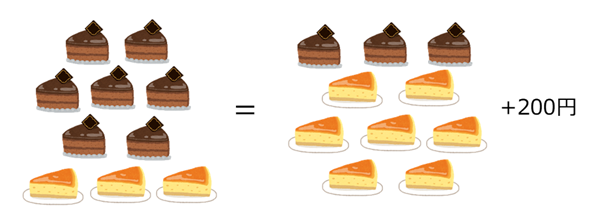
「チョコ7個とチーズ3個」は、「チョコ3個とチーズ7個」より200円高い、ということですね。チョコが多いときのほうが値段が高いのだから、チーズケーキのほうが安いと考えられます。が、それ以上のことは、パッとはわかりにくいですね。

ということで、まずは、具体的に値段をあてはめて計算をしてみましょう。10円刻みとは書いてないですが、チョコレートケーキの値段320円から10円ずつ値段を下げて合計金額を計算してみます。

チーズケーキの値段	チョコ7個チーズ3個の合計金額	チョコ3個チーズ7個の合計金額	差額
310	3170	3130	40
300	3140	3060	80
290	3110	2990	120
280	3080	2920	160
270	3050	2850	200
260	3020	2780	240

書き並べると、上のようになります。チーズケーキの金額を下げるほど、差額は大きくなっていき、チーズケーキが270円のときに、差額がちょうど200円になることがわかります。これよりも下げると、差額はより大きくなることから、結局、チーズケーキは270円だったんだな、ということがわかります。

こうして答えは求まりましたが、なんだかたまたま見つかった感じがしますね。チーズケーキがもし100円だったら、見つけるのは相当大変でした。また、10円刻みじゃなかったら、1円刻みで調べることになるので、もっと大変です。もし、値段ではなく重さなどであれば、答えは小数の可能性もあります。見つけるのは無理だったかもしれません。

もう少しいい方法はないでしょうか。

状況をシンプルに言い換えていこう

さて、先ほどは、「チョコ7個とチーズ3個」は、「チョコ3個とチーズ7個」より200円高い、という状況を考えました。チョコが320円だったら、チーズはいくらになるかを考えていました。

ここで、状況をよく考えてみると、チョコレートケーキを買う量を同じだけ減らしても、差は変わらないですね。なので、チョコを買う個数を3個ずつ減らしてみましょう。すると、状況はシンプルになります。

　「チョコ4個とチーズ3個」は、「チーズ7個」より200円高い

ことがわかるでしょう。同様に、チーズケーキを買う個数を同じだけ減らしても、差額は変わりません。さらにシンプルになります。

　「チョコ4個」は、「チーズ4個」より200円高い

ことがわかります。4個同士の金額の差がわかっているのだから、1個同士の差もわかりますね。4個ずつ買ったときの差が200円なのだから、1個ずつ買ったときの差は50円になります。つまり、

　「チョコ1個」は、「チーズ1個」より50円高い

ことがわかります。チョコ1個は320円なので、チーズケーキの値段は、 $320-50=270$ 円だとわかりますね。

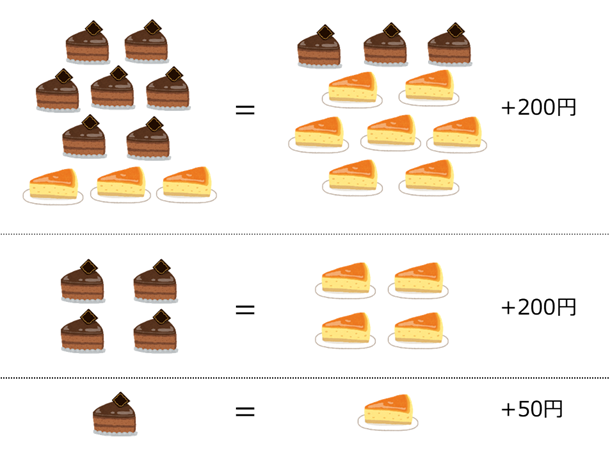
はじめは、「チョコ7個チーズ3個」と「チョコ3個チーズ7個」の比較をしていましたが、よく考えると「チョコ4個」と「チーズ4個」の比較ができるようになり、最終的に「チョコ1個」と「チーズ1個」の比較ができるようになります。こうして、「たまたま」ではなく、「確実に」答えを見つけることができるようになります。たとえ1円刻みであったとしても、見つけることができますね。

文字式を使って表してみよう

先ほど、言葉で説明していた内容を、文字を使った式で表すと、より短く表現できます。

チーズケーキ1個の値段を $x$ 円としてみましょう。先ほどの内容を式で書いていくと、次のようになります。

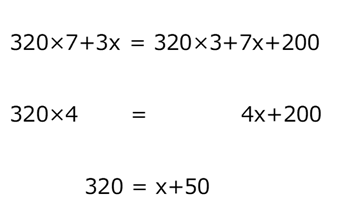
1行目の式は、「チョコ7個とチーズ3個」が「チョコ3個とチーズ7個」より200円高いことを表す式です。ここから、チョコ3個ずつを取り除き、チーズ3個ずつを取り除いても、やはり200円高いことに変わりはないですね。それを表しているのが2行目の式です。4個ずつの値段の差がわかったので、4で割ったのが3行目の式です。こうして、 $x=270$ 、つまり、チーズケーキ1個の値段が270円であることが求められます。

ただ、式の場合は、もう少し簡単に計算することができます。一番はじめの式\[ 320\times7 +3x = 320\times 3+7x+200 \]で、両辺から $1160$ を取り除けば、右辺から数字だけの項がなくなります。\[ 1080+3x=7x \]さらに $3x$ を両辺から引いて\[ 1080=4x \]ここで、4で割ると $x=270$ となります。

はじめの頃は、文字を使った式で考えるよりも、言葉での説明で考えたほうがわかりやすく感じるかもしれません。しかし、文字を使った式で考えていくほうが、将来、より複雑な状況も扱えるようになっていきます。このようにして、わからない値（上の問題のケースではチーズケーキの値段のことです）を求めるために使う等式のことを、方程式といいます。今後は、この方程式の扱い方を見ていきます。