【応用】方べきの定理の逆(2本の弦)
ここでは、方べきの定理の逆について見ていきます。
方べきの定理の逆
【基本】方べきの定理(2本の弦)で見たように、方べきの定理とは次のような内容です。
実は、方べきの定理の逆も成り立ちます。ただ、そのときの結論は何になるか、少しわかりにくいですね。答えをかくと、円の存在です。つまり、4点が同一円周上にあることです。
方べきの定理の逆は、次のような内容です。
点 $\mathrm{P}$ が2つの線分の交点のときも、線分の延長線上の交点のときも成り立ちます。
方べきの定理の逆は、4点が同一円周上にあることを示す場合などで使えることがあります。
方べきの定理の逆の証明
それでは証明していきましょう。
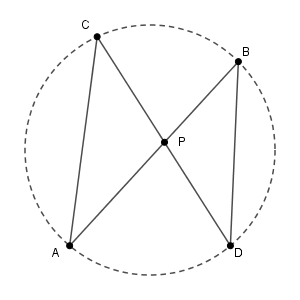
まず、点 $\mathrm{P}$ が2つの線分の交点の場合を考えます。
条件より $\mathrm{PA}\cdot\mathrm{PB} = \mathrm{PC}\cdot\mathrm{PD}$ だから $\mathrm{PA}:\mathrm{PD} = \mathrm{PC}\cdot\mathrm{PB}$ が成り立ちます。また、 $\angle \mathrm{APC}=\angle \mathrm{DPB}$ が成り立ちます。2組の辺の比とその間の角がそれぞれ等しいので、 $\triangle \mathrm{PAC}$ ∽ $\triangle \mathrm{PDB}$ がいえます。
これより、 $\angle \mathrm{PAC}=\angle \mathrm{PDB}$ が言えます。 $\angle \mathrm{BAC}=\angle \mathrm{BDC}$ なので、円周角の定理の逆(参考:【基本】四角形が円に内接するための条件 の前半)から、4点 $\mathrm{A,B,C,D}$ が同一円周上にあることが示せました。
一方、点 $\mathrm{P}$ が2つの線分の延長線上の交点の場合を考えます。
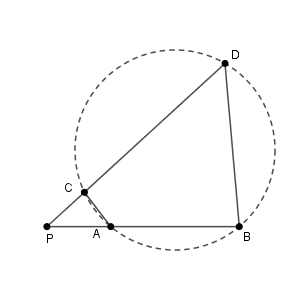
この場合も途中までは同じで、 $\angle \mathrm{PAC}=\angle \mathrm{PDB}$ が言えます。これより、四角形 $\mathrm{ABDC}$ がある円に内接することがいえます(参考:【基本】四角形が円に内接するための条件 )。なので、4点 $\mathrm{A,B,C,D}$ が同一円周上にあることが示せました。
例題
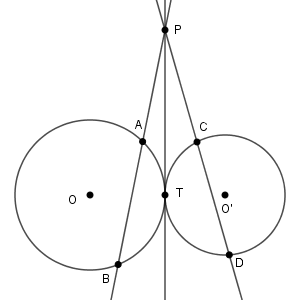
直線 $\mathrm{PT}$ の左側と右側にはなんの関係もなさそうに見えます。なので、4点が同一円周上にあるというのは不思議に感じるかもしれませんが、方べきの定理の逆を使えば示すことができます。
まず、方べきの定理を使います(逆ではなくて)。そうすると、次の2つが成り立ちます。
\begin{eqnarray}
\mathrm{PA}\cdot \mathrm{PB} &=& \mathrm{PT}^2 \\[5pt]
\mathrm{PC}\cdot \mathrm{PD} &=& \mathrm{PT}^2 \\[5pt]
\end{eqnarray}この2つから、\[ \mathrm{PA}\cdot \mathrm{PB}=\mathrm{PC}\cdot \mathrm{PD} \]が成り立つので、方べきの定理の逆から、4点 $\mathrm{A,B,C,D}$ が同一円周上にあることが示せました。
実際、次のように円をかくことができます。わかりやすいように、赤い円を追加してみました。
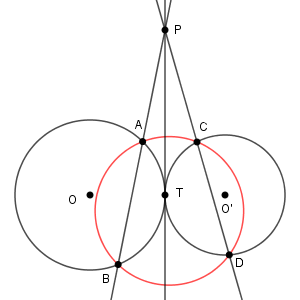
$\mathrm{P}$ から円 $\mathrm{O,O'}$ に引いた直線(接線じゃない方)を動かすと、4点は動き、赤い円も変化しますが、4点が同一円周上にあること自体は変わりません。
おわりに
ここでは方べきの定理の逆について見てきました。方べきの定理とは異なり、円が見えていないことがあるので、使いどころが難しいかもしれません。4点が同一円周上にあることを示す場合などで使えることがあるので、そのような場合に試してみましょう。





