【基本】接弦定理

🕒 2022/08/28 🔄 2023/05/01

ここでは、円の接線と弦の作る角に関する、ある性質について見ていきます。

📘 目次

接弦定理

次のように、直線 $\ell$ が点 $\mathrm{A}$ で円 $\mathrm{O}$ に接しているとします。また、円周上に点 $\mathrm{B}$ をとります。

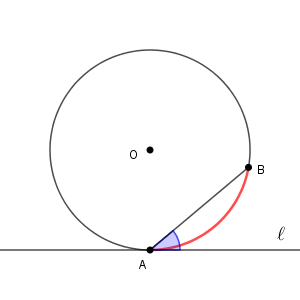
このとき、接線 $\ell$ と弦 $\mathrm{AB}$ が作る角（青い角）は、この角の内部にある弧（赤い部分の弧）に対する円周角と等しくなります。つまり、次の図のように点 $\mathrm{P, T}$ をとったときに、青い角 $\angle \mathrm{BAT}$ と赤い角 $\angle \mathrm{APB}$ が等しくなる、ということです。

なぜそうなるかは、次のように示せます。線分 $\mathrm{AC}$ が直径になるように点 $\mathrm{C}$ をとります。

半円に対する円周角なので $\angle \mathrm{ABC}=90^{\circ}$ になることに注意しましょう。

こうすると、
\begin{array}{llll} & & \angle \mathrm{APB} \\[5pt] &=& \angle \mathrm{ACB} & (\textsf{円周角の定理}) \\[5pt] &=& 90^{\circ} -\angle \mathrm{CAB} & (\triangle \mathrm{ABC} \textsf{に着目}) \\[5pt] &=& \angle \mathrm{BAT} & (\mathrm{AC}\perp \mathrm{AT} \textsf{より}) \\[5pt] \end{array}となるので、たしかに一致します。

これは $\angle \mathrm{BAT}$ が鋭角のときの証明です。直角の場合は、次のようになります。

このときは、 $\angle \mathrm{APB}$ は半円に対する円周角なので $90^{\circ}$ だから、 $\angle \mathrm{BAT}=\angle \mathrm{APB}$ となります。

$\angle \mathrm{BAT}$ が鈍角の場合は次のようになります。点 $\mathrm{S}$ を次のようにとります。

このとき、前半で示した鋭角のケースが使えて、 $\angle \mathrm{ABP}=\angle \mathrm{PAS}$ となります。よって
\begin{array}{llll} & & \angle \mathrm{APB} \\[5pt] &=& 180^{\circ} -\angle \mathrm{PAB} -\angle \mathrm{ABP} & (\triangle \mathrm{ABP} \textsf{に着目}) \\[5pt] &=& 180^{\circ} -\angle \mathrm{PAB} -\angle \mathrm{PAS} & (\textsf{鋭角のケース}) \\[5pt] &=& \angle \mathrm{BAT} & \\[5pt] \end{array}となるので、たしかに一致します。

こうして、どのケースでも成り立つことが示せました。この定理は、接弦定理(alternate segment theorem) と呼ばれています。

接弦定理

円の接線とその接点を通る弦が作る角は、その角の内部にある弧に対する円周角と等しい。

言葉にすると難しいですが、図を見て理解しましょう。

例題

次の図の $\alpha$ を求めなさい。

二等辺三角形の底角がわかっているので\[ \angle \mathrm{A}=180^{\circ}-55^{\circ} \times 2=70^{\circ} \]となります。接弦定理から、 $\alpha=70^{\circ}$ となります。

もう少し詳しく書くと次のようになります。 $\alpha$ は接線と弦 $\mathrm{BC}$ との作る角の大きさです。この角の内部にある弧とは、弧 $\mathrm{BC}$ のことです。 $\angle \mathrm{A}$ は、この弧に対する円周角なので、接弦定理から $70^{\circ}$ だとわかる、ということです。