【基本】方べきの定理(2本の弦)
ここでは、円の2つの弦に関する、方べきの定理について見ていきます。
方べきの定理その1
円にはいい性質がいろいろあるので、等しい角や相似な図形が見つかりやすくなります。
例えば、次のような、2つの弦 $\mathrm{AB}$, $\mathrm{CD}$ が、円の内部で交わるとしましょう。交点を $\mathrm{P}$ とおきます。
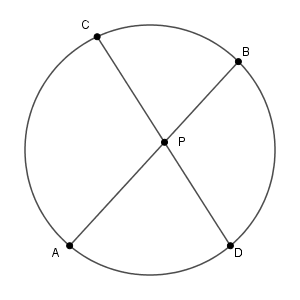
このとき、 $\triangle\mathrm{PAC}$ と $\triangle \mathrm{PDB}$ について考えてみます。円周角の定理から、次の2つが成り立ちます。
\begin{eqnarray}
\angle \mathrm{ACP} &=& \angle \mathrm{DBP} \\[5pt]
\angle \mathrm{CAP} &=& \angle \mathrm{BDP} \\[5pt]
\end{eqnarray}
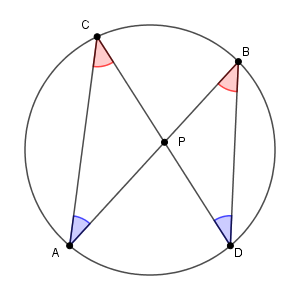
2組の角がそれぞれ等しいので、$\triangle\mathrm{PAC}$ ∽ $\triangle \mathrm{PDB}$ です。このことから、 $\mathrm{PA}:\mathrm{PC}=\mathrm{PD}:\mathrm{PB}$ となるので\[ \mathrm{PA}\cdot\mathrm{PB} = \mathrm{PC}\cdot\mathrm{PD} \]が成り立ちます。
この等式が成り立つことを、方べきの定理(power of a point theorem) といいます。
方べきの定理その2
先ほど、方べきの定理について見ましたが、実は2つの弦の交点が円の外にあるときにも同じ式が成り立ちます。
次のような、2つの弦 $\mathrm{AB}$, $\mathrm{CD}$ があって、これらの弦を含む直線が円の外部で交わるとしましょう。交点を $\mathrm{P}$ とおきます。
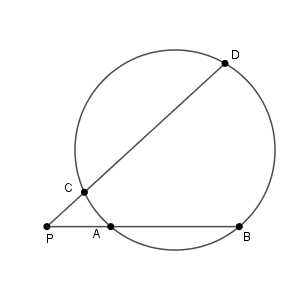
今回は円周角の定理は使わないですが、先ほどと同じように角が等しいことがわかります。四角形 $\mathrm{ABCD}$ が円に内接することから、 $\triangle\mathrm{PAC}$ と $\triangle \mathrm{PDB}$ において、次の2つが成り立ちます。
\begin{eqnarray}
\angle \mathrm{ACP} &=& \angle \mathrm{DBP} \\[5pt]
\angle \mathrm{CAP} &=& \angle \mathrm{BDP} \\[5pt]
\end{eqnarray}
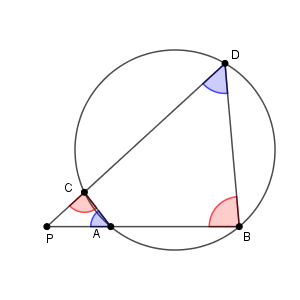
2組の角がそれぞれ等しいので、$\triangle\mathrm{PAC}$ ∽ $\triangle \mathrm{PDB}$ となるので\[ \mathrm{PA}\cdot\mathrm{PB} = \mathrm{PC}\cdot\mathrm{PD} \]が成り立ちます。
この内容も方べきの定理といいます。
まとめると、次のようになります。
交点が円の内部にあるときと外部にあるときしか示していませんが、円周上にあるときは両辺が $0$ になるので、この場合も成り立つと言えます(変なケースなので、円周上にあるケースは除外することもあります)。
これを利用して例題を解いてみましょう。
例題
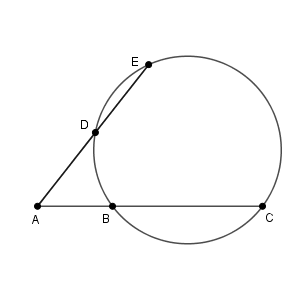
2つの弦 $\mathrm{BC, DE}$ を延長したものが点 $\mathrm{A}$ で交わっている、という状況なので、方べきの定理が使えます。どういう等式が成り立つのか、対応をよく見て間違えないようにしましょう。今の場合は、次の式が成り立ちます。\[ \mathrm{AB}\cdot\mathrm{AC} = \mathrm{AD}\cdot\mathrm{AE} \]わかっている条件から、 $\mathrm{AB}=4$, $\mathrm{AC}=4+8=12$, $\mathrm{AD}=5$ なので、
\begin{eqnarray}
4\cdot12 &=& 5\cdot \mathrm{AE} \\[5pt]
\mathrm{AE} &=& \frac{48}{5} \\[5pt]
\end{eqnarray}となります。求めるのは $\mathrm{DE}$ なので、\[ \mathrm{DE}=\frac{48}{5}-5=\frac{23}{5} \]が答えとなります。
この問題で、 $\mathrm{AB}\cdot\mathrm{BC}$ と $\mathrm{AD}\cdot\mathrm{DE}$ が等しい、とやってしまう間違いが多いです。方べきの定理で出てくる線分は、片方の端点は弦の交点(今の場合は $\mathrm{A}$ のこと)です。間違えないようにしましょう。
わからなくなってしまったら、円に内接する四角形を作った証明を思い出しましょう。
おわりに
ここでは方べきの定理について見てきました。弦が交わるだけで使えるので、使える場面は多そうです。交点が円の外にあるときは、どの線分を使うのか間違えやすいので注意しましょう。





