【基本】ベクトルの成分

🕒 2017/08/16 🔄 2023/05/01

ここでは、ベクトルの成分表示について見ていきます。

📘 目次

ベクトルの成分の導入

【基本】ベクトルなどで見てきた通り、ベクトルは、「どちらの向きか」「どのくらいの長さか」で表されます。長さのことは、「ベクトルの大きさ」と言って、 $|\overrightarrow{ \mathrm{ AB } }|$ などで表します。これは AB の長さのことです。

一方、向きはどのように表せばいいでしょうか。上とか左とかならいいですが、右下などといわれても、向きはいろいろありますよね。

そこで、ベクトルの向きを表す方法として、「成分」というものを使います。内容は単純で、単に、上下方向と左右方向に分けて表現するだけです。例えば、「右に3、下に2の向き」などといった感じです。

ただ、ここで、少しひっかかる人もいるかもしれません。【導入】ベクトルを考える意味についてでは、ベクトルは「斜めの軸を使えばいい」という新しい発想が使えたはずなのに、結局、縦と横の軸を使うのか、と。

しかし、「斜めの軸が使えること」と「向きを表現するために縦横の軸を使うこと」は、何も矛盾しません。これは、「斜めの軸の世界」を「縦横の軸の世界」と関連付けることができることを表しており、むしろ、「ベクトルの世界と座標の世界を行き来できる」というメリットのある話なんですね。

具体的にどういったメリットがあるかは、これからいろいろ学んでいきながら実感できると思います。

単位ベクトル

まず、ベクトルの成分の話をする前に、単位ベクトルの話をします。

単位ベクトル(unit vector) とは、大きさが $1$ のベクトルです。

例えば、 $\vec{0}$ でないベクトル $\vec{a}$ があったとしましょう。この大きさ $|\vec{a}|$ でこのベクトルを割ると、長さが $1$ になりますね。よって、\[ \frac{\vec{a} }{|\vec{a}|} \]は、 $\vec{a}$ と平行な単位ベクトル、となります。また、\[ -\frac{\vec{a} }{|\vec{a}|} \]も、向きは逆ですが、 $\vec{a}$ と平行な単位ベクトルです。

大きさが $1$ なので、目盛りのような役割りで使われることがあります。

基本ベクトル

単位ベクトルのうち、右を向いているもの（x 軸に平行）と上を向いているもの（y 軸に平行）を、基本ベクトル(standard unit vectors) といい、それぞれ、 $\vec{e_1}$, $\vec{e_2}$ で表します。

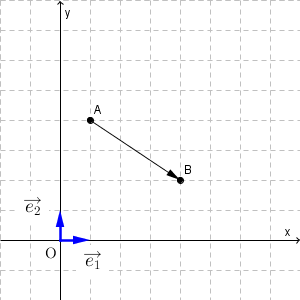
例えば、上の図の $\overrightarrow{ \mathrm{ AB } }$ について考えてみましょう。目盛りの間隔は $1$ とします。目盛りから、右に3, 下に2の向きであることがわかりますね。そのため、\[ \overrightarrow{ \mathrm{ AB } }=3\vec{e_1}-2\vec{e_2} \]と書くことができます。

【基本】ベクトルの分解で見たことからわかるとおり、どんなベクトル $\vec{p}$ も、 $\vec{e_1}$, $\vec{e_2}$ を使って\[ \vec{p}=s\vec{e_1}+t\vec{e_2} \]と1通りに表すことができます。この対応を使って、 $\vec{p}$ の向きを表します。 $s,t$ を $\vec{p}$ の成分と言い、 s を x 成分、 t を y 成分といいます。

さらに、ベクトルを次のようにも書きます。\[ \vec{p}=(s,t) \]このような表示を、成分表示といいます。例えば、上の例であれば\[ \overrightarrow{ \mathrm{ AB } }=(3,-2) \]となります。

座標みたいな書き方ですが、座標とは違う点に注意してください。これはベクトルの場所を表しているのではなく、ベクトルの向きと大きさを表しています。例えば、下の図を見てみましょう。

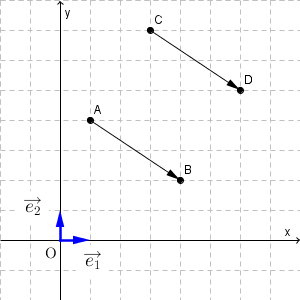
上の図で、 $\overrightarrow{ \mathrm{ AB } }$ と $\overrightarrow{ \mathrm{ CD } }$ を成分表示すると、どちらも $(3,-2)$ となり、一致します。場所を表す座標とは違う、ということをおさえておきましょう。このことからもわかる通り、ベクトルが等しいということは、ベクトルの成分が等しいということと同値です。

なお、
\begin{eqnarray} \vec{e_1} &=& (1,0) \\[5pt] \vec{e_2} &=& (0,1) \\[5pt] \vec{0} &=& (0,0) \end{eqnarray}となります。