【標準】ベクトルの成分と大きさの最小値

🕒 2017/08/24 🔄 2024/07/06

ここでは、ベクトルの成分を使って、ベクトルの大きさの最小値を求める問題を考えます。また、この問題の図形的な意味についても見ていきます。

📘 目次

ベクトルの成分とベクトルの大きさの最小値

例題

$\vec{a}=(3,1)$, $\vec{b}=(2,-1)$ のとき、 $|\vec{a}+t\vec{b}|$ の最小値を求めなさい。

【基本】ベクトルの成分と演算で見たように、ベクトルの大きさは、成分を使って表すことができます。そのため、まず成分について考えましょう。

成分は
\begin{eqnarray} \vec{a}+t\vec{b} &=& (3,1)+t(2,-1) \\ &=& (3+2t,1-t) \\ \end{eqnarray}となります。そして、各成分を2乗して足したものが、ベクトルの大きさの2乗となります。なので、 \begin{eqnarray} |\vec{a}+t\vec{b}|^2 &=& (3+2t)^2+(1-t)^2 \\[5pt] &=& 9+12t+4t^2+1-2t+t^2 \\[5pt] &=& 5t^2+10t+10 \\[5pt] &=& 5(t+1)^2+5 \\[5pt] \end{eqnarray}となります。このあたりの計算は、【基本】二次関数の最大・最小などでやりましたね。

上のグラフから $t=-1$ のときに $|\vec{a}+t\vec{b}|^2$ は最小値 $5$ をとります。 $|\vec{a}+t\vec{b}|$ は0以上の値しかとらないので、 $t=-1$ のときに最小値をとることがわかり、その値は $\sqrt{5}$ となります。

成分を用いて大きさを表現した後は、二次関数の問題として考えていけばいいですね。

図形的な意味

先ほどの例題は、計算だけで解くことができるのですが、図形的に考えることも重要です。ここでは、図形的な意味について見ていきます。

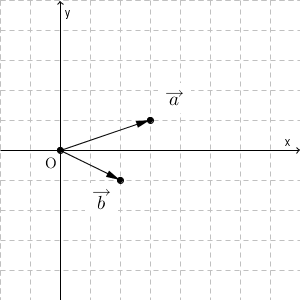
$\vec{a}$, $\vec{b}$ は、上の図のようになります。原点を基準にしています。このとき、 $\vec{a}+t\vec{b}$ はどうなるかを考えてみます。

$\overrightarrow{ \mathrm{ OA } }=\vec{a}$, $\overrightarrow{ \mathrm{ OB } }=\vec{b}$ となるように、点 A, B をとりましょう。 $t\vec{b}$ は $\vec{b}$ と平行なベクトルを表すことから、 $\overrightarrow{ \mathrm{ OP } }=\vec{a}+t\vec{b}$ となるように点 P をとれば、 P は「A を通り、 OB に平行な直線」の上にあることがわかります。この直線のことを l と書くことにしましょう。

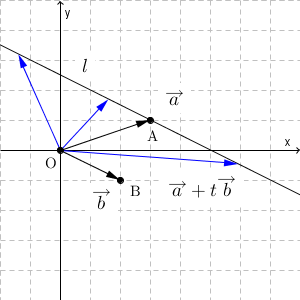
「 P が直線 l の上にある」という見方も大事なのですが、これを踏まえて $|\vec{a}+t\vec{b}|$ について考えることも大事です。これは、今までの言葉で書くと、 OP の長さのことですね。つまり、「直線 l 上の点で、原点から一番近いとき」というのが、 $|\vec{a}+t\vec{b}|$ が最小になるときと一致します。これは「点 P が、原点から直線 l に下した垂線と直線 l との交点に一致するとき」であることがわかります。

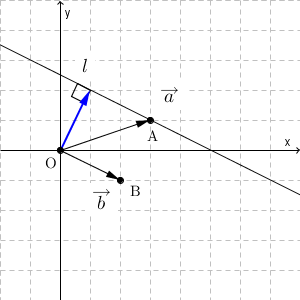
図形的に考えた場合、ベクトルと点の座標が対応していること、ベクトルの t 倍が直線に対応していること、ベクトルの大きさが原点からの距離に対応していること、といった見方ができるわけですね。その結果、先ほどの例題で考えた「ベクトルの大きさが最小となるとき」というのは、原点から直線に引いた垂線の足に対応していることがわかります。

このように、図形とベクトルとを対応させて考えることは、ベクトルを理解するうえでも大事ですし、ベクトルを使って図形の問題を解くときなどにも役立ちます。