【基本】三角比と角の二等分線
ここでは、三角比の分野で出題される、角の二等分線とからめた問題を見ていきます。
三角比と角の二等分線
角の二等分線とは、角を同じ大きさに分ける線のことです。下の図で言うと、 AD が $\angle \mathrm{ A }$ の二等分線です。
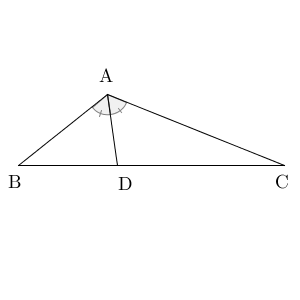
有名な性質として、 $\mathrm{ AB }:\mathrm{ AC }=\mathrm{ BD }:\mathrm{ CD }$ になる、というものがあります。次のように、 C を通り、 AD に平行な線をひくと、わかりやすいです。この線と AB との交点を E としましょう。
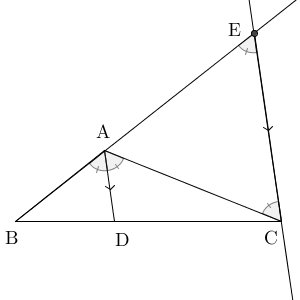
$\triangle \mathrm{ ABD }$ と $\triangle \mathrm{ EBC }$ は相似なので、 $\mathrm{ AB }:\mathrm{ AE }=\mathrm{ BD }:\mathrm{ CD }$ となります。また、 $\angle \mathrm{ AEC }=\angle \mathrm{ ACE }$ なので、 $\mathrm{ AE }=\mathrm{ AC }$ となり、 $\mathrm{ AB }:\mathrm{ AC }=\mathrm{ BD }:\mathrm{ CD }$ が得られます。
三角比の問題で角の二等分線が出てくる理由は、
- 辺の比を利用して、余弦定理などを使う
- 外接円とからめて、円周角の定理などを使う
- 面積や内接円の性質を使う
例題
図をかくと、こうなります。
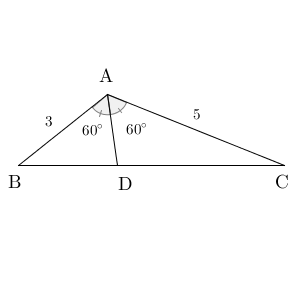
一般的には余弦定理を使って解くのですが、この問題はすごくわかりやすい角度なので、特殊な解き方ができます。三角形の面積に着目します。
【基本】三角比と三角形の面積で見た通り、 $\triangle \mathrm{ ABC }$ の面積は次のように書けます。\[ \frac{1}{2} \mathrm{ AB }\cdot\mathrm{ AC }\sin\angle \mathrm{ BAC }=\frac{15\sqrt{3} }{4} \]
一方、この三角形を2つの三角形の和だと考えることもできます。すると、 $\triangle \mathrm{ ABC }$ の面積は次のようにも書けます。
\begin{eqnarray}
& &
\frac{1}{2}\mathrm{AB}\cdot\mathrm{AD}\sin\angle\mathrm{BAD}
+\frac{1}{2}\mathrm{AC}\cdot\mathrm{AD}\sin\angle\mathrm{CAD} \\[5pt]
&=&
\frac{3\sqrt{3}\mathrm{AD} }{4} +\frac{5\sqrt{3}\mathrm{AD} }{4} \\[5pt]
&=&
2\sqrt{3}\mathrm{AD} \\[5pt]
\end{eqnarray}
この2つは同じ値なので、
\begin{eqnarray}
2\sqrt{3}\mathrm{AD} &=& \frac{15\sqrt{3} }{4} \\[5pt]
\mathrm{AD} &=& \frac{15}{8} \\[5pt]
\end{eqnarray}と求められます。
おわりに
ここでは、角の二等分線の簡単な復習と、三角比とからめた問題の例を見ました。
上の例題では、 $\angle \mathrm{ A }=120^{\circ}$ となっていて、この三角比も、半分の角の三角比も、両方とも具体的に値を求めることができるため、上のような解き方ができます。しかし、一般的にはこんなにきれいに三角比が求められる問題は少ないです。より一般的な問題は別のページ(【標準】三角比と角の二等分線)で見ることにします。





