【基本】円の接線
ここでは、円の接線について見ていきます。
円と直線の位置関係
円と直線の位置関係は、次の3つのパターンがあります。
1つ目は、2点で交わるパターンです。
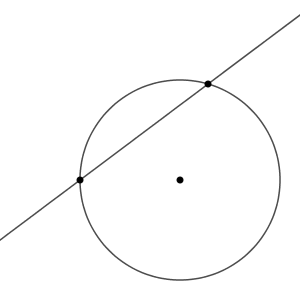
このとき、直線上の点で、円の中心から一番近い点は円の内側にあります。なので、2点で交わることがわかります。
直線が円の中心からどんどん遠ざかっていくと、2つの交点が一致する瞬間がやってきます。このとき、円と直線の共有点は1点だけになります。
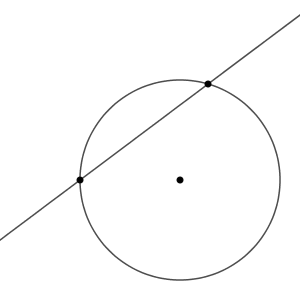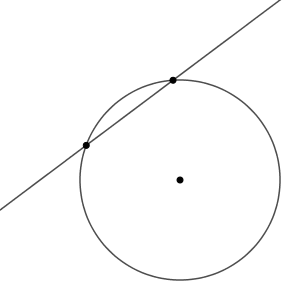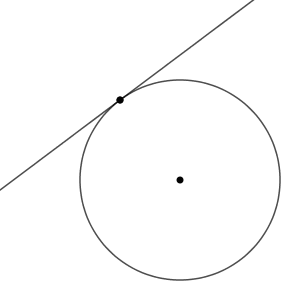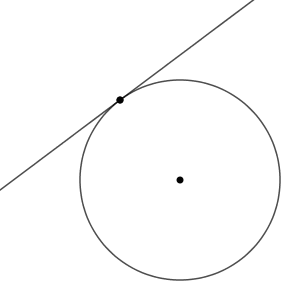
このとき、直線上の点で、円の中心から一番近い点が共有点になります。つまり、共有点と円の中心を結んだ線分は、この直線と垂直である、ということです。
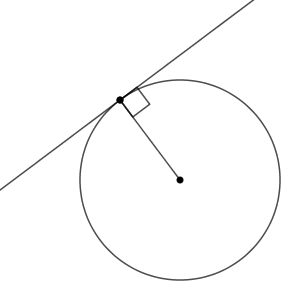
さらに直線が円の中心から遠ざかると、共有点はなくなります。
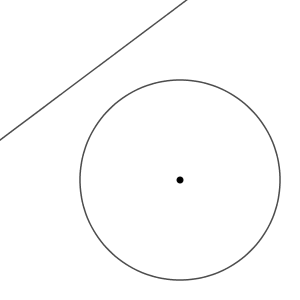
この3つの位置関係の中で、2つ目が一番重要です。このケースには特別な名前がついています。
また、途中の図でも見ましたが、直線 $\ell$ が円 $\mathrm{O}$ と点 $\mathrm{A}$ で接するとき、 $\ell \perp \mathrm{OA}$ が成り立ちます。
逆に、円 $\mathrm{O}$ と直線 $\ell$ との共有点 $\mathrm{A}$ に対して $\ell \perp \mathrm{OA}$ であれば、直線 $\ell$ は円 $\mathrm{O}$ の接線になります。
接線の長さ
次のように、円 $\mathrm{O}$ の外にある点 $\mathrm{P}$ から、接線をひくことを考えましょう。
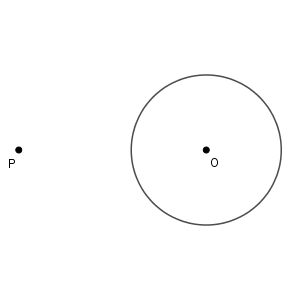
もし接線が引けたとして、接点を $\mathrm{A}$ とすると、 $\angle \mathrm{PAO}$ は $90^{\circ}$ になります。なので、このような点が見つかればいいですね。
実は、このような点は必ず存在します。線分 $\mathrm{OP}$ を直径とする円をかきます。この円は円 $\mathrm{O}$ と2点で交わります(点$\mathrm{O}$ は円$\mathrm{O}$ の内側、点$\mathrm{P}$ は外側にあるので)。そこで、それぞれ $\mathrm{A,B}$ と名前をつけることにします。
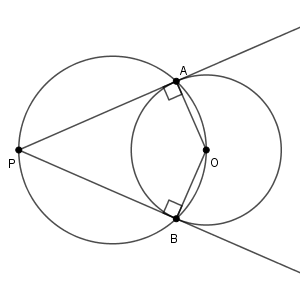
半円に対する円周角なので、 $\angle \mathrm{OAP}=\angle \mathrm{OBP}=90^{\circ}$ です。なので、直線 $\mathrm{AP}$ も直線 $\mathrm{BP}$ も円 $\mathrm{O}$ の接線となります。
このように、円の外にある点からは、2本の接線をひくことができます。このとき、この点から接点までの長さを、接線の長さ といいます。
$\triangle \mathrm{OAP}$ と $\triangle \mathrm{OBP}$ は合同です(直角三角形で、斜辺と他の1辺がそれぞれ等しいため)。そのため、 $\mathrm{AP}=\mathrm{BP}$ だから、2つの接線の長さは等しいことがわかります。
例題
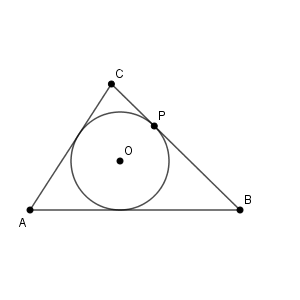
他の接点にも次のように名前をつけます。
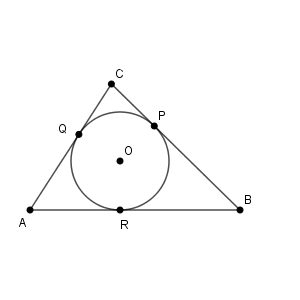
$\mathrm{BP}$ の長さは $6-2=4$ です。接線の長さが等しいことを使うと、 $\mathrm{BR}=4$ です。
また、接線の長さが等しいことを再び使って、 $\mathrm{CQ}=\mathrm{CP}=2$ となることがわかります。なので、もう一度使って、 $\mathrm{AR}=\mathrm{AQ}=5-2=3$ です。
以上から、 $\mathrm{AB}$ の長さは $4+3=7$ と求められます。
おわりに
ここでは、円の直線について見てきました。例題で見たように、接線の長さが等しいことは、三角形の内接円とからめて出題されることがあります。





