🏠 Home / 数学C / 平面上の曲線 / 二次曲線

【基本】二次曲線と直線

🕒 2018/04/19 🔄 2023/05/01

ここでは、二次曲線と直線との共有点について見ていきます。

📘 目次

二次曲線と直線との共有点

例題1

双曲線 $x^2-y^2=1$ と直線 $x+2y=0$ との共有点の座標を求めなさい。

グラフは次のようになっています。

共有点は、双曲線の方程式も直線の方程式も両方を満たすということなので、連立させて解けば求められます。

直線の方程式から $x=-2y$ なので、これを双曲線の方程式に代入して
\begin{eqnarray} (-2y)^2-y^2 &=& 1 \\[5pt] 3y^2 &=& 1 \\[5pt] y &=& \pm\frac{\sqrt{3} }{3} \\[5pt] \end{eqnarray}となります。 $x=-2y$ であることから、共有点の座標は\[ \left(\frac{2\sqrt{3} }{3},-\frac{\sqrt{3} }{3}\right), \left(-\frac{2\sqrt{3} }{3},\frac{\sqrt{3} }{3}\right) \]となります。

放物線と直線との共有点、楕円と直線との共有点の場合も、求め方は同じです。連立させて解きます。 $x,y$ の片方を消すように変形すると、片方の文字に関する二次方程式が出来上がります。これを解けばいいですね。

なお、二次方程式が出てくるため、共有点の個数は、最大でも2個であることがわかります。

二次曲線と直線との共有点の数

例題2

k を定数とする。楕円 $x^2+2y^2=2$ と直線 $y=2x+k$ との共有点の個数を答えなさい。

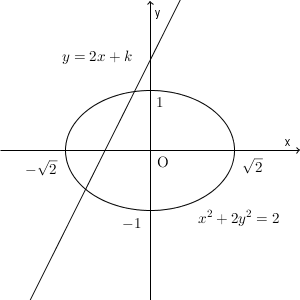
これも、先ほどと同様に、連立させて考えていきます。直線の方程式の内容を楕円の方程式に代入すると
\begin{eqnarray} x^2+2(2x+k)^2 &=& 2 \\[5pt] 9x^2+8kx+2k^2-2 &=& 0 \\[5pt] \end{eqnarray}となります。この実数解1つに対して、直線の方程式に代入すれば、1つの共有点の座標が対応します。なので、この実数解の個数と共有点の個数は一致します。なので、実数解の個数を考えましょう。

といっても、ただの二次方程式なので、判別式を調べるだけです（参考：【基本】二次方程式の解の個数と判別式）。判別式は
\begin{eqnarray} & & (8k)^2-4\cdot 9\cdot (2k^2-2) \\[5pt] &=& 64k^2-72k^2+72 \\[5pt] &=& -8(k-3)(k+3) \\[5pt] \end{eqnarray}となります。

よって、判別式が正となる $-3\lt k \lt 3$ のときは共有点は2個、 $k=\pm 3$ のときは共有点は1個、 $k\lt -3, k\gt 3$ のときは共有点なし、となります。これが答えです。

ちなみに、この例題で、 $k=\pm 3$ のときは、図は次のようになっています。

このように、二次曲線と直線の共有点が1点のとき、言い換えれば、直線の方程式から1文字を消去して二次曲線の方程式に代入した方程式が重解を持つとき、この直線はこの二次曲線に接するといい、この直線を二次曲線の接線といいます。また、このときの共有点を接点といいます。これらの用語は、二次関数のときと同じです。