【基本】方べきの定理（接線）

🕒 2022/09/01 🔄 2023/05/01

ここでは、接線に関する方べきの定理について見ていきます。

📘 目次

方べきの定理の復習

【基本】方べきの定理（2本の弦）で見たように、方べきの定理とは、以下の図で $\mathrm{PA}\cdot\mathrm{PB} = \mathrm{PC}\cdot\mathrm{PD}$ が成り立つことをいいます。

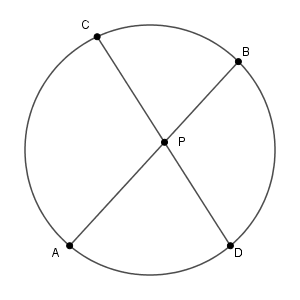
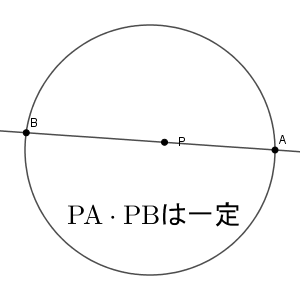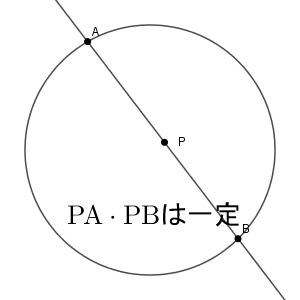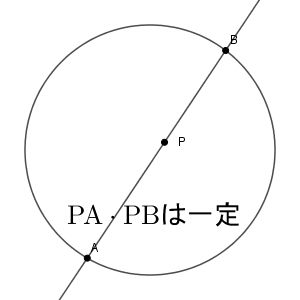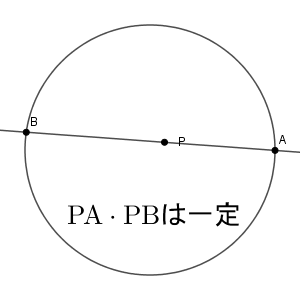
ここで、見方を変えてみましょう。2本の弦ではなく、交点の $\mathrm{P}$ を基準にしてみます。点 $\mathrm{P}$ を固定して、この点を通るように弦 $\mathrm{AB}$ を動かしてみます。このとき、方べきの定理から、 $\mathrm{PA}\cdot \mathrm{PB}$ の値が一定になる、といえます。

また、方べきの定理には、弦の交点が円の外側にあるバージョンもあるのでした。

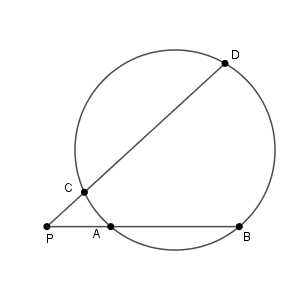
この場合でも、先ほどと同じ式\[ \mathrm{PA}\cdot\mathrm{PB} = \mathrm{PC}\cdot\mathrm{PD} \]が成り立ちます。

このバージョンでも、見方を変えてみます。円の外にある点 $\mathrm{P}$ を固定して、この点を通り、円と2点で交わるように動かします。このときにできる弦を $\mathrm{AB}$ とすると、 $\mathrm{PA}\cdot \mathrm{PB}$ の値が一定になります。

方べきの定理は、このように見ることもできるんですね。

方べきの定理その３

さて、方べきの定理を別の見方から見てみましたが、2つ目のバージョンについてもう一度考えてみます。

円の外にある点から直線を引いた場合、円と2点で交わることもありますが、1点だけを共有することもあります。接するときですね（【基本】円の接線）。この場合について考えてみます。

このときは、弦の長さが短くなって1点になってしまった、とも考えられます。

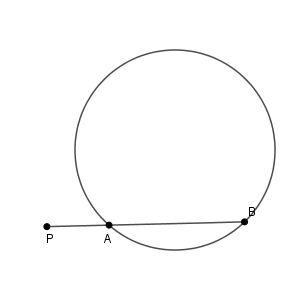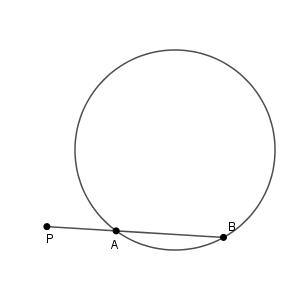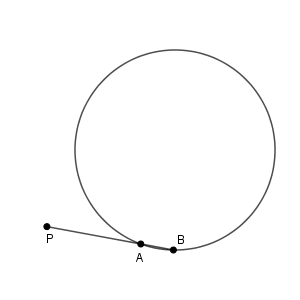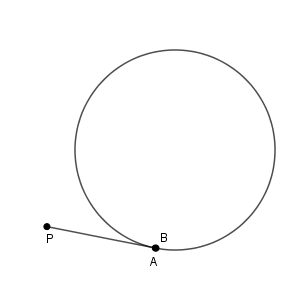
ということは、この場合も $\mathrm{PA}\cdot \mathrm{PB}$ の値は一定になると予想できます。実際にそうなのか、確かめてみましょう。

次のような状況を考えてみます。

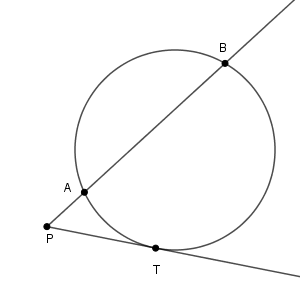
直線 $\mathrm{PT}$ は円に接していて、点 $\mathrm{T}$ は接点とします。このとき、 $\mathrm{PA\cdot PB}=\mathrm{PT}^2$ となることを示してみます。

次のように線を結びます。

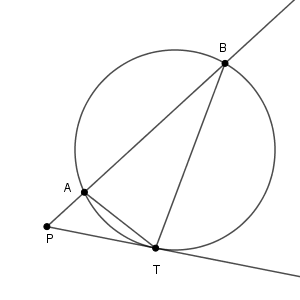
このとき、 $\triangle \mathrm{PTA}$ と $\triangle \mathrm{PBT}$ について、 $\angle \mathrm{P}$ が共通であることがわかります。また、接弦定理から、\[ \angle \mathrm{PTA}=\angle \mathrm{PBA} \]が成り立ちます（参考：【基本】接弦定理）。こうして、 $\triangle \mathrm{PTA}$ ∽ $\triangle \mathrm{PBT}$ となることがわかるので、\[ \mathrm{PT:PA}=\mathrm{PB:PT} \]より、\[ \mathrm{PA\cdot PB}=\mathrm{PT}^2 \]となることが示せました。

この内容も、方べきの定理といいます。

方べきの定理

円の外部にある点 $\mathrm{P}$ から円に引いた接線の接点を $\mathrm{T}$ とする。また、$\mathrm{P}$ を通り、この円と2点 $\mathrm{A, B}$ で交わる直線を引く。このとき、以下が成り立つ。\[ \mathrm{PA}\cdot\mathrm{PB} = \mathrm{PT}^2 \]

これを利用して例題を解いてみましょう。

例題

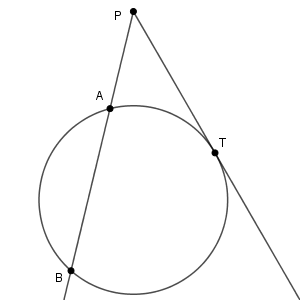
次の図で、直線 $\mathrm{PT}$ は円の接線で、 $\mathrm{T}$ は接点です。また、 $\mathrm{AB}=5$, $\mathrm{AP}=3$ です。$\mathrm{PT}$ の長さを求めなさい。

方べきの定理を使いますが、点の対応に注意しましょう。\[ \mathrm{PT}^2=\mathrm{PA\cdot PB}=3\cdot 8=24 \]なので、 $\mathrm{PT}=2\sqrt{6}$ が答えです。間違って $\mathrm{PA\cdot AB}$ を計算しないように注意しましょう。