【基本】一次不等式と一次関数のグラフ

🕒 2016/08/24 🔄 2023/05/01

ここから二次不等式について見ていきますが、その前に一次不等式の例を使って、「グラフを使った不等式の解き方」を見ていきます。この考え方は、二次不等式を解くときに必要になってきます。

📘 目次

一次不等式を、式変形で解く

次のような一次不等式を考えます。\[ -2x +6 \gt 0 \]これは、【基本】一次不等式の解き方でみたように、次のように解けばいいですね。
\begin{eqnarray} -2x+6 & \gt & 0 \\ -2x & \gt & -6 \\ x & \lt & 3 \\ \end{eqnarray}マイナスの数を掛けたり割ったりしたときに不等号の向きが変わることに気をつければ、一次方程式と同じような方法で解くことができます。

一次不等式を、グラフを使って解く

上の不等式を、次のようにグラフを使って考えてみましょう。

$y=-2x+6$ という直線を考えてみます。また、例として $x=1,5$ での点もとってみます。

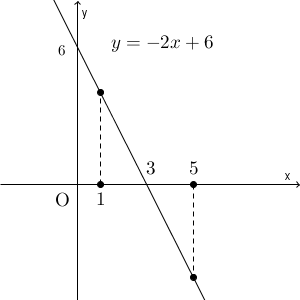
$x=1$ のとき、この直線上の点は x 軸より上にあります。つまり、この直線上の点の y 座標（ $-2x+6$ ）は、0より大きいということです。よって、このときは $-2x+6 \gt 0$ が成り立つことがわかります。

一方、 $x=5$ のときは、この直線上の点は x 軸より下にあります。同じように考えれば、このときは $-2x+6 \gt 0$ は成り立たない、ということがわかりますね。

では、 $-2x+6 \gt 0$ が成り立つ範囲はどこになるかを考えましょう。これは、グラフで言えば、直線上の点 $(x,-2x+6)$ と x 軸上の点 $(x,0)$ を比べたときに、直線上の点の方が上にあるとき、ということです。

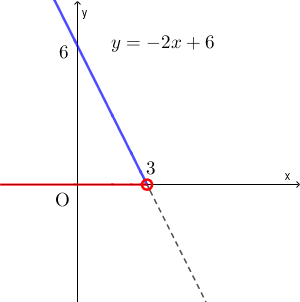
なので、グラフから $x \lt 3$ のときであることがわかります。当たり前ですが、式変形をして得られた冒頭の解き方と同じ答えになります。

グラフを使って不等式を解くには、まずはグラフが正しくかいて x 軸との交点を求めることが必要です。 $ax+b \gt 0$ なら、 $y=ax+b$ のグラフをかき、グラフが x 軸より上にあるような x の範囲が答えになります。 $ax+b \lt 0$ なら、下にある範囲が答えになる、ということですね。