【基本】数列の極限

ここでは、数列の極限、収束と発散について見ていきます。

数列の極限

以前学んだ数列の分野では、漸化式などから第 n 項がどんな式で表されるかを求めることが多かったですね。ただ、状況によっては、途中ではなく、ずっと進んでいったその先がどうなっているか、最終的にどういう値に近づいていくのか、ということが重要となる場合もあります。

数列の極限とは、この「数列の項がずっと進んでいったその先の値」のことです。この値がどういうときに確定するか、確定するならどんな値か、を中心に考えていきます。

以後、数列の極限について考える場合は、項がいつまでも続く、無限数列を前提として考えていきます。

数列の収束

具体的な数列を使って考えてみます。

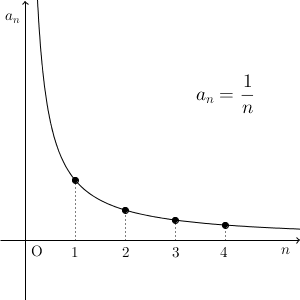
例えば、一般項が\[ a_n=\dfrac{1}{n} \]で表される数列 $\{a_n\}$ があったとしましょう。この数列の項は、 n が大きくなっていくにつれてどんどん小さくなり、最終的には0に近づいていきます。下の図は、 $y=\dfrac{1}{x}$ のグラフ上に、 $x$ が正の整数となる点をとっていったものです。

また、\[ b_n=\dfrac{(-1)^n}{n} \]という数列 $\{b_n\}$ の場合は、負の値と正の値をとりながら、最終的には、やはり0に近づいていきます。

このように、数列がある値に限りなく近づくとき、この数列は収束(convergent) するといい、その値のことを極限値(limit) とか極限といいます。

ここで出てきた $\lim$ という記号は、微分のところでも出てきています（参考：【基本】極限値と微分係数）。また、 $\infty$ は、「無限大」と呼び、「どんな実数よりも大きいもの」を表します。

先ほどの例を記号を使って表せば、
\begin{eqnarray} & & \lim_{n\to\infty} \frac{1}{n} = 0 \\[5pt] & & \lim_{n\to\infty} \frac{(-1)^n}{n} = 0 \\[5pt] \end{eqnarray}となります。

また、この $\lim$ という記号を使わずに、「 $n\to\infty$ のとき $a_n\to\alpha$ 」といった書き方をするときもあります。

なお、定数の値だけをとる数列、例えば、一般項が $c_n=1$ という数列 $\{c_n\}$ に対しては、「 $1$ に限りなく近づく」という言葉は少し変に感じますが、この場合も\[ \lim_{n\to\infty}c_n=1 \]と書きます。途中から1つの値をとる数列の場合も同様です。

数列の発散

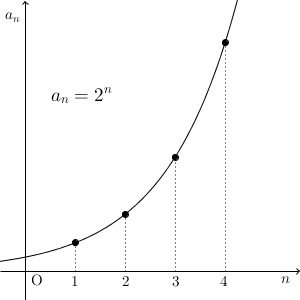
先ほどは、数列が収束する場合、つまり、ある値にどんどん近づいていく場合を見ましたが、必ずしもそうなるとは限りません。例えば、 $a_n=2^n$ であれば、この数列の項は限りなく大きくなっていきます。

また、 $a_n=(-1)^n$ のときも、ある値に近づくとはいえません。

このように、数列が収束しない場合は、発散(divergent) するといいます。上の2つのケースは、どちらも発散する例です。

発散するもののうち、限りなく大きくなる場合は、「正の無限大に発散する」といい、\[ \lim_{n\to\infty}a_n =\infty \]と表します。逆に、 $a_n=-n^2$ のときのように、限りなく小さくなっていく場合は、「負の無限大に発散する」といい、\[ \lim_{n\to\infty}a_n =-\infty \]と表します。

$a_n=(-1)^n$ の例は、正の無限大に発散するわけでも、負の無限大に発散するわけでもありません。このように、収束もしないし、正の無限大にも負の無限大にも発散しないものは、振動する、といいます。\[ a_n=(-2)^n \]も振動する例です。

おわりに

ここでは、数列の極限、収束や発散について見ました。具体的に極限値を求めるには計算練習が必要ですが、まずは言葉の内容を理解しておきましょう。