【基本】共通部分と和集合

🕒 2016/06/17 🔄 2023/05/01

ここでは、2つの集合の「どちらにも含まれている要素の集合」と「どちらかに含まれている要素の集合」について見ていきます。

📘 目次

共通部分

2つの集合A, Bのどちらにも属している要素全体の集合を、共通部分(intersection)と呼びます。「Aの要素、かつ、Bの要素」の集合ということです。

例えば $A=\{1,2,3,6\}$ と $B=\{1,2,4,8\}$ の場合を考えます。それぞれ、6の正の約数、8の正の約数、という集合です。このとき、この2つの共通部分は $\{1,2\}$ となります。どちらの集合にも属しているのは、この2つの要素だけですね。

「共通部分」は、共通集合、積集合、交わりなどと呼ばれることもあります。また、記号を使って $A\cap B$ と書きます。

もちろん、共通部分がない場合もあります。そのときは、【基本】部分集合で紹介したように、空集合を使います。例えば \[ \{1,3,5\} \cap \{ 2,4 \}=\varnothing\]となります。

共通部分があるときは、「交わる」といい、共通部分がないときは、「交わらない」や「互いに素」と言います。

和集合

2つの集合A, Bの少なくとも一方に属している要素全体の集合を、和集合(union)といいます。「Aの要素、または、Bの要素」ということです。両方に属していてもいいです。

例えば $A=\{1,2,3,6\}$ と $B=\{1,2,4,8\}$ のとき、この2つの和集合は $\{1,2,3,4,6,8\}$ となります。なお、【基本】集合と要素に関する、まぎらわしい話でも書いた通り、同じ要素は1回しか書きません。

「和集合」は、記号を使って $A\cup B$ と書きます。

ベン図

集合を考えるときに、次のような図を使うとわかりやすくなることがあります。

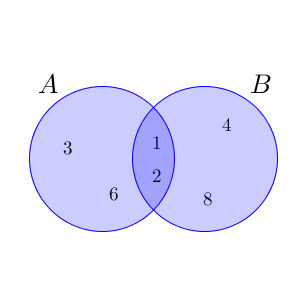
これは $A=\{1,2,3,6\}$ と $B=\{1,2,4,8\}$ のときを図示したものです。このような図をベン図(Venn diagram)と言います。ベンというのは、この図を考え出した数学者の名前です。

円の重なっている部分が、共通部分 $A\cap B$ にあたります。また、色のついている部分全体が、和集合 $A\cup B$ にあたります。

今は状況が簡単なので、ベン図のありがたみがわかりにくいかもしれません。しかし、複雑になってきたときには、ベン図をかいて考えると状況が把握しやすくなります。覚えておきましょう。

記号の覚え方

$\cap$ が共通部分、 $\cup$ が和集合ですが、似ていて覚えづらいですね。

僕は次のようにして覚えています。共通部分というのは、両方に入っているので「かつ」です。「か」の一画目や「つ」の文字を見ると、上の方が丸まっているので、同じく上側が丸い $\cap$ が共通部分だな、と。

和集合の場合は、少なくとも一方に入っているので「または」です。「ま」の文字を見ると、下の方が丸まっているので、同じく下側が丸い $\cup$ が和集合だな、と。

まー、覚えられればどんな覚え方でもOKです。僕の場合は、こうやって関連付けて覚えてる、という紹介でした。

3つ以上の集合の場合

共通部分、和集合は、3つ以上の集合についても考えることができます。

$A\cap B\cap C$ と書けば、3つすべての集合に含まれる要素全体の集合のことです。 $A\cup B \cup C$ であれば、3つのうち少なくともどれか1つの集合に含まれている要素全体の集合のことです。

例えば、次のような例を考えてみます。
\begin{eqnarray} A &=& \{1,2,3,6\} \\ B &=& \{1,2,4,8\} \\ C &=& \{1,3,4,5\} \\ \end{eqnarray}ベン図を描けば次のようになります。

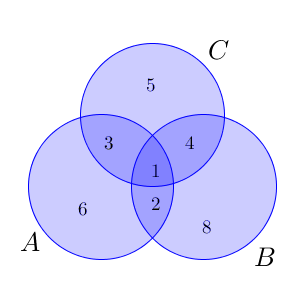
このことから、共通部分（3つが重なっている、一番色の濃い部分）と和集合（色のついている部分）は次のようになることが分かります。
\begin{eqnarray} A\cap B\cap C &=& \{1\} \\ A\cup B\cup C &=& \{1,2,3,4,5,6,8\} \\ \end{eqnarray}