【基本】不等式の性質と数直線

ここでは、不等式の性質を数直線を用いて確認していきます。なお、数直線については、【基本】絶対値の中で登場しているので、そちらも参照してみましょう

不等式の両辺に数を足す場合

数直線とは、直線上の点と実数とを対応させたものでしたね。これを使って、「$a\lt b$ ならば $a+c\lt b+c$」を図示すると、次のようになります。

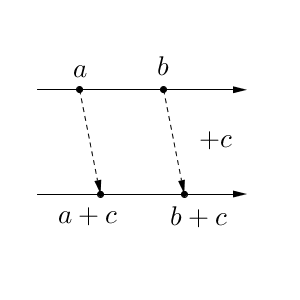
図の上側の数直線が、「$a\lt b$」を表していて、下側の数直線が足した後の「$a+c\lt b+c$」を表しています。同じだけスライドするのだから、大小関係が変わらないことは明らかですね。

引き算のときも同様です。同じだけ左にスライドするので、大小関係は変わりません。

不等式の両辺に正の数を掛ける場合

掛け算の場合は、正か負かで状況が変わるんでしたね。これも数直線を使って考えてみます。まずは、「$0\lt a\lt b$, $c\gt 0$ のとき、$ac\lt bc$」となることを図でかいてみます。

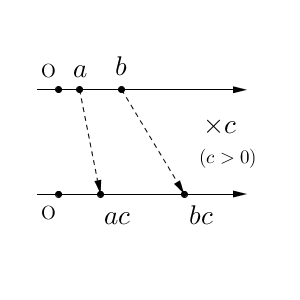
正の数を掛けても、原点から遠かった点は遠いままです。大きい数字は大きいままなので、大小関係は変わりません。

$a,b$ が両方とも負の場合も同様で、大小関係は変わりません。$a\lt 0 \lt b$ のときは、原点の右にある点、左にある点の位置関係は変わらないので、大小関係が変わらないこともわかります。

不等式の両辺に負の数を掛ける場合

では、負の数を掛ける場合を見てみます。「$0\lt a\lt b$, $c\lt 0$ のとき、$ac\gt bc$」となることを図でかいてみます。

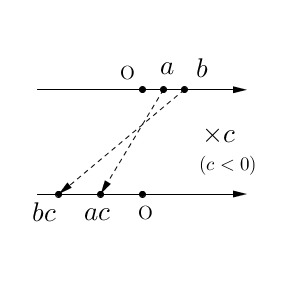
負の数を掛けたため、左右の位置関係が逆転します。原点から遠い点は遠いままですが、反対サイドに行ってしまうため、今回は大小関係が逆転してしまうんですね。

$a,b$ が両方負の場合も、同様に位置関係が逆転します。

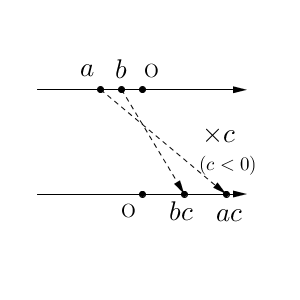
左側にあった点が右側に、右側にあった点が左側に移動するので、大小関係が逆転してしまうことが分かります。

片方が正で片方が負の場合も、同じように図をかけば、2つの点の位置が入れ替わり、大小関係が逆転することが分かるでしょう。

おわりに

ここでは、不等式の性質を数直線を使って確認しました。

数直線を使えば、不等式の性質、つまり、両辺に数字を足し引きした場合、掛けたり割った場合に不等号の向きがどうなるかが理解しやすくなります。負の数を掛けたり負の数で割った場合に、原点から見て反対側に移動してしまうことから、大小関係が逆転することもわかりますね。