【基本】絶対値のついた一次関数のグラフ

🕒 2020/07/04 🔄 2023/05/01

ここでは、絶対値のついた一次関数のグラフをかく問題を見ていきます。

📘 目次

絶対値のついた一次関数のグラフその１

例題1

次の関数のグラフをかきなさい\[ y=|2x+5| \]

2本の縦線で囲っている部分は、絶対値を表しています。絶対値とは、【基本】絶対値でも見たように、絶対値記号の中身が0以上ならそのまま、負ならマイナスをつけたものです。なので、絶対値の記号の中身の符号によって場合分けをして考えていきます。

絶対値記号の中身 $2x+5$ が $0$ 以上になるとき、つまり、 $x\geqq -\dfrac{5}{2}$ のときは、 $|2x+5|=2x+5$ です。一方、中身が負になるとき、つまり、 $x\lt -\dfrac{5}{2}$ のときは、 $|2x+5|=-2x-5$ です。まとめると、
\begin{eqnarray} y = \begin{cases} 2x+5 & \left(x\geqq -\dfrac{5}{2}\right) \\ -2x-5 & \left(x\lt -\dfrac{5}{2}\right) \\ \end{cases} \end{eqnarray}となります。【基本】区分ごとに定義された関数のグラフで見たように、このようなグラフは、範囲ごとにグラフをかいてつなげればいいので、グラフは次のようになります。

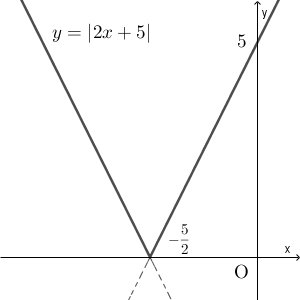
このグラフからもわかる通り、 $y=|2x+5|$ のグラフは $y=2x+5$ のグラフで、 $x$ 軸より下にある部分を折り返した形になっています。これは、絶対値の記号をはずすときに、中身が負ならマイナスをつけて外すことに対応しています。

一般に、 $y=|f(x)|$ の形の関数のグラフは $y=f(x)$ のグラフの $x$ 軸より下の部分を折り返したものになります。

絶対値のついた一次関数のグラフその２

例題2

次の関数のグラフをかきなさい\[ y=|x+1|+|2x-4| \]

今度は $y=|f(x)|$ の形ではないので、折り返しでグラフをかくことはできません。グラフをかくには、場合を分けて絶対値をはずす必要があります。

1つ目の絶対値の中身 $x+1$ は、 $x\geqq -1$ なら0以上、 $x\lt -1$ なら負です。2つ目の絶対値の中身 $2x-4$ は $x\geqq 2$ なら0以上、 $x\lt 2$ なら負です。

以上のことを踏まえると、以下のように3つに分ければいいことがわかります。

まず、 $x\lt -1$ のケースです。この場合、どちらの絶対値も、中身は負なので
\begin{eqnarray} y&=&|x+1|+|2x-4|\\[5pt] &=&-(x+1)-(2x-4)\\[5pt] &=&-3x+3 \end{eqnarray}となります。 $-1\leqq x\lt 2$ の場合、1つ目の絶対値の中身は0以上になるので \begin{eqnarray} y&=&|x+1|+|2x-4|\\[5pt] &=&(x+1)-(2x-4)\\[5pt] &=&-x+5 \end{eqnarray}となります。最後に、 $x\gt 2$ の場合、どちらの絶対値も中身は0以上になるので \begin{eqnarray} y&=&|x+1|+|2x-4|\\[5pt] &=&(x+1)+(2x-4)\\[5pt] &=&3x-3 \end{eqnarray}となります。

以上のことから、それぞれの範囲でグラフをかいて足し合わせれば、次のようにグラフをかくことができます。