【応用】絶対値のついた二次方程式と実数解の個数
ここでは、絶対値のついた二次方程式の実数解の個数を調べる問題を考えていきます。
絶対値のついた二次方程式と実数解の個数
ここでは、グラフを用いて考えてみましょう。【標準】二次関数のグラフと直線との共有点で見たように、グラフの共有点の個数と実数解の個数を対応させて考えます。
$k$ の値は決まっていないし、扱いづらいので、 $k$ とそれ以外というようにわけると考えやすくなります。つまり、 $y=|x^2-3x|-x$ と $y=k$ のグラフを使って、グラフの共有点を考えるようにします。
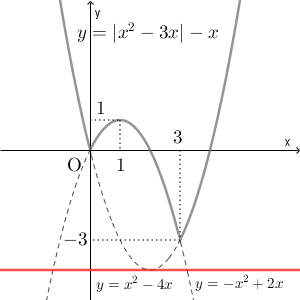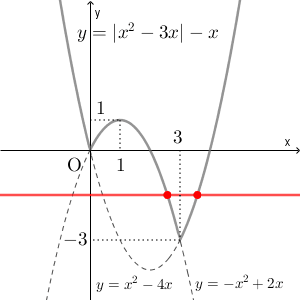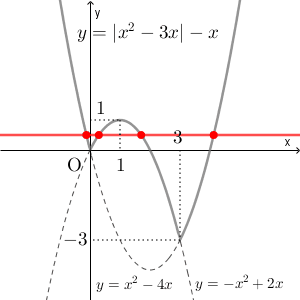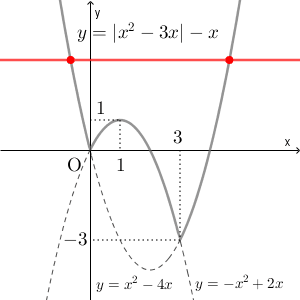
$y=|x^2-3x|-x$ のグラフは、絶対値の中の符号に注目して場合分けをすればいいのでした(参考:【基本】絶対値のついた二次関数のグラフ)。絶対値の中が0以上となるのは $x\leqq 0$, $x\geqq 3$ のときで、負になるのは $0\lt x\lt 3$ のときです。それぞれ
\begin{eqnarray}
y
&=&
|x^2-3x|-x \\[5pt]
&=&
x^2-3x-x \\[5pt]
&=&
(x-2)^2-4 \\[5pt]
\end{eqnarray}と
\begin{eqnarray}
y
&=&
|x^2-3x|-x \\[5pt]
&=&
-(x^2-3x)-x \\[5pt]
&=&
-(x-1)^2+1 \\[5pt]
\end{eqnarray}なので、 $y=|x^2-3x|-x$ のグラフは次のようになります。

$y=k$ のグラフは $x$ 軸に平行な直線であり、 $k$ の値に応じて $y=|x^2-3x|-x$ との共有点の個数は変化します。赤い線が $y=k$ で、赤い点が共有点を表しています。
こうして、グラフから共有点の個数を考えると、問題文にある方程式の実数解の個数は次のように求められます。
$k\lt -3$ のとき:解なし
$k=-3$ のとき:1個
$-3\lt k\lt 0$ のとき:2個
$k=0$ のとき:3個
$0\lt k\lt 1$ のとき:4個
$k=1$ のとき:3個
$k\gt 1$ のとき:2個
たくさんありますが、全部まとめてこれが答えです。
ちなみに、絶対値とそれ以外というように分けると考えにくくなります。 $|x^2-3x|=x+k$ の実数解を考えるために、 $y=|x^2-3x|$ と $y=x+k$ のグラフの共有点を考えることにします。そうすると、 $k$ によって、グラフは次のように変化します。
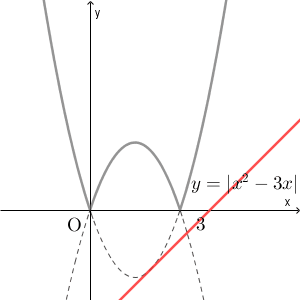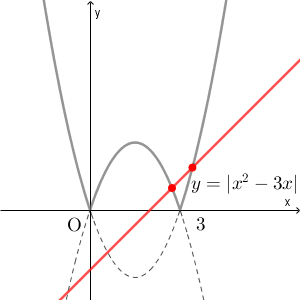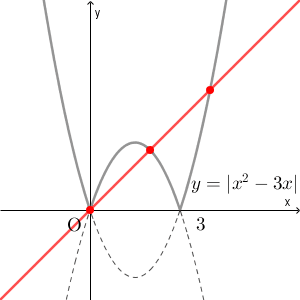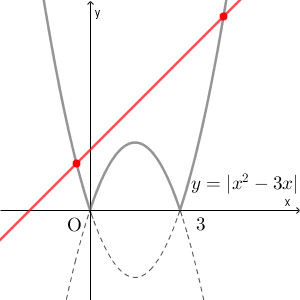
赤い線が $y=x+k$ を表しています。傾いている直線を上下に動かすのは考えにくいし、例えば、共有点の数が4個になるのはどのときか、を考えるのも難しくなってしまいます(できなくはないですが)。可能であれば、動かすものは $x$ 軸に平行な直線にした方がいいでしょう。
おわりに
ここでは、絶対値のついた二次方程式の実数解がいくつあるかを考える問題を見てきました。グラフの共有点の個数を数える、という方針で考えると解きやすくなります。





