【基本】区分ごとに定義された関数のグラフ
ここでは、区分ごとに定義された関数の例と、グラフのかき方を見ていきます。
区分ごとに定義された関数
下の図のような一辺が $4$ の正方形 ABCD があったとします。
今、点 P が頂点 B にいるとして、1秒間に $1$ の速さで、辺の上を通って、頂点 C, D, A の順に移動するとします。このときの、 $x$ 秒後の三角形 ABP の面積 $y$ について考えます。
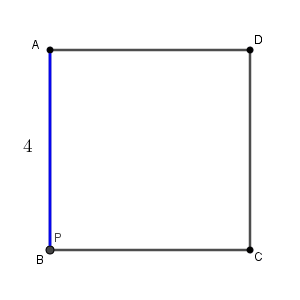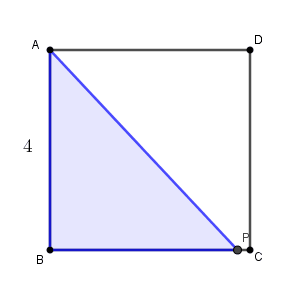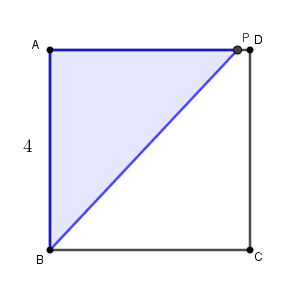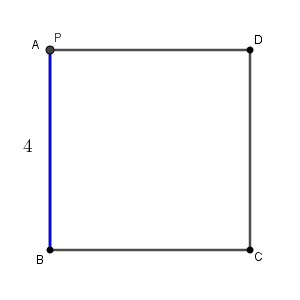
ただし、点 P が A, B にいるときは、 $y=0$ とします。
上の動いている図を見てもわかる通り、状況に応じて三角形の面積の変化の仕方が変わることがわかります。点 P が辺 BC 上にいるときは面積は増え続けますが、 CD 上にいるときは面積は変わりません(形は変わっていますが)。辺 DA 上にいるときは面積は減り続け、最終的に $0$ になります。
このように状況に応じて変化の仕方が変わるので、 $x$ の値に応じて $y$ の表し方が変わってきます。場合を分けて、それぞれのケースで $y$ を $x$ の式で表してみましょう。
まず、点 P が辺 BC 上にいるときです。このようになるのは、 $0\leqq x\leqq 4$ のときですね。辺 AB を底辺と考えれば高さは $x$ なので、\[ y=\frac{4\times x}{2}=2x \]となります。この式は、点 P が頂点 B にいるときも成り立ちます。
次に、点 P が辺 CD 上にいるときを考えます。このようになるのは、 $4\leqq x\leqq 8$ のときです。辺 AB を底辺と考えれば高さは $4$ なので、\[ y=\frac{4\times 4}{2}=8 \]となります。 $x$ に関係なく、同じ値をとり続けます。
最後、点 P が辺 DA 上にいるときを考えます。このようになるのは、 $8\leqq x\leqq 12$ のときです。辺 AB を底辺と考えて高さを考えます。このときの高さは、線分 AP の長さです。
今まで移動してきた BC と CD と DP の和が $x$ だから DP の長さは $x-8$ なので、 AP の長さは $4-(x-8)=12-x$ となります。
こうして\[ y=\frac{4\times (12-x)}{2}=24-2x \]と表せることがわかります。点 P が頂点 A にいるとき、つまり $x=12$ のときは $y=0$ なので、この式は点 P が頂点 A にいるときも成り立ちます。
$x$ の値に応じて $y$ の表し方が異なるときは、次のようにかきます。
\begin{eqnarray}
y
=
\begin{cases}
2x & ( 0\leqq x\lt 4 ) \\
8 & ( 4\leqq x\lt 8 ) \\
24-2x & ( 8\leqq x\leqq 12 ) \\
\end{cases}
\end{eqnarray}このように、 $x$ の値によって表し方が異なるような関数を、区分的に定義された関数や区分的関数(piecewise function) などと呼ぶことがあります。高校数学では特に名前を付けて呼ぶことは少ないですが、こういう関数は今後よく登場します。
なお、区間は重複しないように書くのが一般的です(今のケースだと、 $x=4$ や $x=8$ の場合を重複させないように書く)。
区分ごとに定義された関数のグラフ
先ほどの関数のグラフを考えてみましょう。といっても特に難しいことをするわけではなく、区分ごとにグラフをかいてつなぎ合わせるだけです。
今の場合であれば、 $0\leqq x\lt 4$ の範囲では $y=2x$ のグラフをかき、 $4\leqq x\lt 8$ の範囲では $y=8$ のグラフをかき、 $8\leqq x\lt 12$ の範囲では $y=24-2x$ のグラフをかく、というだけです。次のようになります。
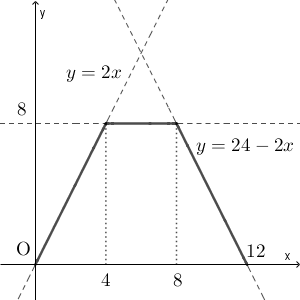
$y=2x$ のグラフは、 $0\leqq x\lt 4$ の範囲は実線でかき、他の部分は点線でかいています。このように範囲外の部分は点線でかいて、グラフの一部だと表すことが多いです。
今のケースでは、三角形の面積は連続的に変化するため、グラフがブチっと切れるようになっていると、関数の表し方かグラフのかき方がおかしいと気づくことができます。
区分ごとに定義された関数のグラフの例
上では三角形の面積について考えましたが、区分ごとに定義された関数のグラフの例は他にもいろいろあります。
身近なものでいえば、タクシーの料金メーターや電車の運賃のように、あるところまでは同じ値、ある地点を超えると値が変わってまたしばらく同じ値、というのを繰り返すものがあります。その場合、グラフは次のようになります。

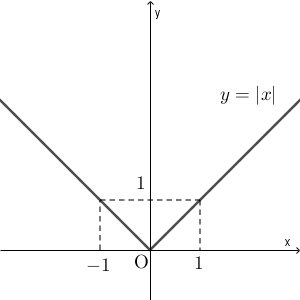
また、今までに出てきた数学の話でいうと、絶対値を使った関数のグラフもそうです。例えば、 $y=|x|$ のグラフは次のようになりますが、詳しくは別の記事で扱います。
おわりに
ここでは、区分ごとに定義された関数とそのグラフについて見てきました。教科書ではわざわざ説明されていないことも多いですが、高校数学ではよく出てくるものなので、これからも頻繁に目にするでしょう。複雑なグラフになりやすいので、試験などでもよく登場します。





